Các giá trị của x thỏa mãn điều kiện của bất phương trình x + 2 3 + x + 3 + 1 x > 2 x - 3 là:
![]()
![]()
![]()
![]()
Tìm các giá trị x thỏa mãn điều kiện của bất phương trình sau: 1 x 2 - 4 ≤ 2 x x 2 - 4 x + 3
BPT xác định khi
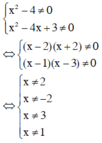
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–2; 1; 2; 3}
Tìm các giá trị x thỏa mãn điều kiện của bất phương trình sau: 2 1 - x > 3 x + 1 x + 4
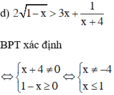
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = (–∞; 1] \ {–4}.
Tìm các giá trị x thỏa mãn điều kiện của mỗi bất phương trình sau: 2 x - 1 + x - 1 3 < 2 x x + 1
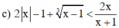
BPT xác định khi x + 1 ≠ 0 ⇔ x ≠ –1.
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–1}
Tìm các giá trị x thỏa mãn điều kiện của bất phương trình sau:
1 x < 1 - 1 x + 1
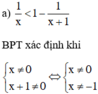
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{0; –1}
Cho phương trình: x²-2(n+1)x+n²+2=0
xác định các giá trị của n để phương trình có hai nghiệm phân biệt x1;x2 thỏa mãn điều kiện: x1³+x2³=1
Δ=(2n+2)^2-4(n^2+2)
=4n^2+8n+4-4n^2-8
=8n-4
Để phương trình có hai nghiệm phân biệt thì 8n-4>0
=>n>1/2
x1^3+x2^3=1
=>(x1+x2)^3-3x1x2(x1+x2)=1
=>(2n+2)^3-3(n^2+2)(2n+2)=1
=>8n^3+24n^2+24n+8-3(2n^3+2n^2+4n+4)=1
=>8n^3+24n^2+24n+8-6n^3-6n^2-12n-12-1=0
=>2n^3+18n^2+12n-5=0
=>\(n\in\varnothing\)
Cho hệ phương trình: x+ay=2 và ax-27=1. Tìm các giá trị của a để hệ phương trình đã cho có nghiệm thỏa mãn điều kiện x>0, y<0.
cho phương tình x2+x-m-2 (ẩn x)
a) tìm các giá trị của m để phương trình có nghiệm
b) tính giá trị của m, khi biết phương trình đã cho có hai nghiệm phân biệt x1,x2 thỏa mãn điều kiện x12 - x1x2 -2x2 = 16
\(\Delta=1-4\left(-m-2\right)\ge0\Leftrightarrow m\ge-\dfrac{9}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1x_2=-m-2\end{matrix}\right.\)
\(x_1^2-x_1x_2-2x_2=16\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)-2x_1x_2-2x_2=16\)
\(\Leftrightarrow-x_1-2\left(-m-2\right)-2x_2=16\)
\(\Leftrightarrow x_1+2x_2=2m-12\)
\(\Rightarrow x_1+x_2+x_2=2m-12\)
\(\Leftrightarrow-1+x_2=2m-12\Rightarrow x_2=2m-11\Rightarrow x_1=-1-x_2=-2m+10\)
Lại có: \(x_1x_2=-m-2\)
\(\Rightarrow\left(-2m+10\right)\left(2m-11\right)=-m-2\)
\(\Leftrightarrow4m^2-43m+108=0\Rightarrow\left[{}\begin{matrix}m=4\\m=\dfrac{27}{4}\end{matrix}\right.\)
Tất cả các giá trị của m để phương trình x^2−2(2m−3)x+4m−3 = 0 có hai nghiệm x1,x2 thỏa mãn điều kiện x1+x2−2x1x2 < 8 là gì?
Online chờ gấp, đa tạ các vị!
Để pt có hai nghiệm <=> \(\Delta\ge0\)\(\Leftrightarrow16m^2-64m+48\ge0\)
\(\Leftrightarrow m\in R\backslash\left(1;3\right)\)
Có \(x_1+x_2-2x_1x_2< 8\)
\(\Leftrightarrow2\left(2m-3\right)-2\left(4m-3\right)< 8\)
\(\Leftrightarrow-4m-8< 0\)
\(\Leftrightarrow m>-2\)
Kết hợp với đk => \(m\in\left(-2;1\right)\cup\left(3;+\infty\right)\cup\left\{1;3\right\}\)
Cho phương trình x^2_mx_2=0.tìm các giá trị của m để Pt có 2 nghiệm x1 và x2 thỏa mãn điều kiện x1x2+2x1+2x2=4
Phương trình là: \(x^2-mx-2=0\) đúng ko em nhỉ?
\(\Delta=m^2+8>0;\forall m\) nên pt đã cho luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=-2\end{matrix}\right.\)
Ta có:
\(x_1x_2+2x_1+2x_2=4\)
\(\Leftrightarrow x_1x_2+2\left(x_1+x_2\right)=4\)
\(\Leftrightarrow-2+2m=4\)
\(\Leftrightarrow2m=6\)
\(\Leftrightarrow m=3\)