Cho a, x là các số thực dương và a ≠ 1 thỏa mãn log a x = log a x . Tìm giá trị lớn nhất của a?
A. 1
B. log 2 e - 1
C. e ln 10 e
D. 10 log e 2
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
![]()
![]()
![]()
![]()
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Đáp án D.
Ta có
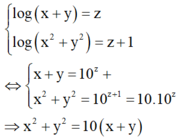
Khi đó
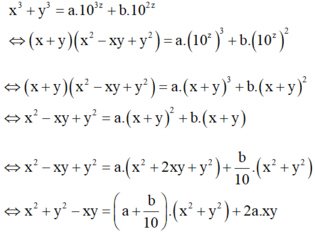
Đồng nhất hệ số, ta được

Giả sử a,b là các số thực sao cho x 3 + y 3 = a 10 3 x + b 10 2 x đúng với mọi các số thực dương x, y, z thỏa mãn log ( x + y ) = z và log ( x 2 + y 2 ) = z + 1 . Giá trị của a+b bằng
A. -31/2
B. -25/2
C. 31/2
D. 29/2
Cho a, b là các số thực dương thỏa mãn log 2 a + log 2 b = 0.
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính l o g ( a 2 b 3 ) ?
A. 6xy
B. x 3 y 3
C. x 3 + y 3
D. 2x+3y
Giả sử a,b là các số thực sao cho x 3 + y 3 = a . 10 3 x + b . 10 2 x đúng với mọi số thực dương x,y,z thỏa mãn log(x+y)=z và log x 2 + y 2 = z + 1 Giá trị của a+b bằng:
A. -31/2
B. -25/2
C. 31/2
D. 29/2
Cho a,b là các số thực thỏa mãn log 2 . log 2 a - log b = 2 . Hỏi a,b thỏa mãn hệ thức nào dưới đây?
A. a = 100b
B. a = 100 - b
C. a = =100 + b
D. a = 100 b
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 x 2 + a 2 - 2 n - 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 , e 2 y = 1 . Số phần tử của S là:
A. 0
B. 1
C. 2
D. Vô số
Cho bốn số thực dương a, b, x, y với \(a,b \ne 1\). Khẳng định nào sau đây là sai?
A. \({\log _a}(xy) = {\log _a}x + {\log _b}y\).
B. \({\log _a}\frac{x}{y} = {\log _a}x - {\log _a}y\).
C. \({\log _a}\frac{1}{x} = \frac{1}{{{{\log }_a}x}}\).
D. \({\log _a}b \cdot {\log _b}x = {\log _a}x\).
Cho hai số thực dương x, y thỏa mãn log x + log y ≥ log ( x 3 + 2 y ) Giá trị nhỏ nhất của P = 25x + y là
A. 375/4
B. 45/2
C. 195/2
D. 14 26