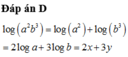Các câu hỏi tương tự
Giả sử a,b là các số thực sao cho
x
3
+
y
3
a
10
3
x
+
b
10
2
x
đúng với mọi các số thực dương x, y, z thỏa mãn
log
(
x
+
y...
Đọc tiếp
Giả sử a,b là các số thực sao cho x 3 + y 3 = a 10 3 x + b 10 2 x đúng với mọi các số thực dương x, y, z thỏa mãn log ( x + y ) = z và log ( x 2 + y 2 ) = z + 1 . Giá trị của a+b bằng
A. -31/2
B. -25/2
C. 31/2
D. 29/2
Giả sử a,b là các số thực sao cho
x
3
+
y
3
a
.
10
3
x
+
b
.
10
2
x
đúng với mọi số thực dương x,y,z thỏa mãn log(x+y)z và
log
x
2
+...
Đọc tiếp
Giả sử a,b là các số thực sao cho x 3 + y 3 = a . 10 3 x + b . 10 2 x đúng với mọi số thực dương x,y,z thỏa mãn log(x+y)=z và log x 2 + y 2 = z + 1 Giá trị của a+b bằng:
A. -31/2
B. -25/2
C. 31/2
D. 29/2
Cho hai số thực dương x, y thỏa mãn
log
x
+
log
y
≥
log
(
x
3
+
2
y
)
Giá trị nhỏ nhất của P 25x + y là A. 375/4 B. 45/2 C. 195/2 D.
14
26
Đọc tiếp
Cho hai số thực dương x, y thỏa mãn log x + log y ≥ log ( x 3 + 2 y ) Giá trị nhỏ nhất của P = 25x + y là
A. 375/4
B. 45/2
C. 195/2
D. 14 26
Cho các số thực dương x, y, z và thỏa mãn x + y + z 3. Biểu thức
P
x
4
+
y
4
+
8
z
4
đạt GTNN bằng
a
b
, trong đó a, b là các số tự nhiên dương,
a
b
là phân số tối giản. Tính a - b A. 234. B. 523. C. 235. D. 525.
Đọc tiếp
Cho các số thực dương x, y, z và thỏa mãn x + y + z = 3. Biểu thức P = x 4 + y 4 + 8 z 4 đạt GTNN bằng a b , trong đó a, b là các số tự nhiên dương, a b là phân số tối giản. Tính a - b
A. 234.
B. 523.
C. 235.
D. 525.
Cho a,b là các số thực thỏa mãn log 2 . log 2 a - log b = 2 . Hỏi a,b thỏa mãn hệ thức nào dưới đây?
A. a = 100b
B. a = 100 - b
C. a = =100 + b
D. a = 100 b
Cho a,b,c là các số thực dương thỏa mãn
a
log
5
2
4
,
b
log
4
6
1
,
log
,
c
log
7
3
49
Tính giá trị của biểu thức
T
a...
Đọc tiếp
Cho a,b,c là các số thực dương thỏa mãn a log 5 2 = 4 , b log 4 6 = 1 , log , c log 7 3 = 49 Tính giá trị của biểu thức T = a log 2 2 5 + b log 4 2 6 + 3 c log 7 2 3
A. T=126
B. T = 5 + 2 3
C. T=88
D. T = 3 - 2 3
Cho hàm số
y
ln
2
x
-
a
-
2
m
ln
2
x
-
a
+
2
(m là tham số thực), trong đó x,...
Đọc tiếp
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 ; e 2 y = 1 . Số phần tử của S là:/
A. 0
B. 1
C. 2
D. Vô số
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
9
x
+
y
4
và
x
y
-
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = - a + b 2 với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 32
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
9
x
+
y
4
và
x
y
−
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = − a + b 2 , với a, b là các số nguyên dương. Tính a+b
A. 14
B. 3
C. 21
D. 32