Tìm nguyên hàm của hàm số y = f(x) = c o s 3 x .
A. ∫ f ( x ) d x = cos 4 x x + C
B. ∫ f ( x ) d x = 1 4 sin 3 x 3 + 3 sin x + C
C. ∫ f ( x ) d x = 1 12 sin 3 x - 3 4 sin x + C
D. ∫ f ( x ) d x = cos 4 x . sin x 4 + C
Những câu hỏi liên quan
Tìm nguyên hàm của hàm số
f
(
x
)
2008
+
ln
2
x
x
có dạng
F
(
x
)
a
ln
x
+
ln
x
3
b
+
C
. Khi đó tổng S a + b là? A. 2012 B. 2010 C. 2009 D. 2011
Đọc tiếp
Tìm nguyên hàm của hàm số f ( x ) = 2008 + ln 2 x x có
dạng F ( x ) = a ln x + ln x 3 b + C . Khi đó tổng S
= a + b là?
A. 2012
B. 2010
C. 2009
D. 2011
Tìm nguyên hàm của hàm số
f
(
x
)
2008
+
ln
2
x
x
có dạng
F
(
x
)
a
ln
x
+
ln
3
x...
Đọc tiếp
Tìm nguyên hàm của hàm số f ( x ) = 2008 + ln 2 x x có dạng F ( x ) = a ln x + ln 3 x b + C Khi đó tổng S = a+b là?
A. 2012
B. 2010
C. 2009
D. 2011
Bải 1: Tìm tập xác định của các hàm số
sau:
a)
3x-2
2x+1
c) y=\sqrt{2x+1}-\sqrt{3-x}
b) y=
²+2x-3
d) y=
√2x+1
X
f(x)
Chú ý: * Hàm số cho dạng v
thi f(x) * 0.
ở Hàm số cho dạng y = v/(x) thì f(r) 2 0.
X
* Hàm số cho dạng " J7(p) thi f(x)>0.
a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)
Đúng 0
Bình luận (0)
F(x) là nguyên hàm của hàm số
f
(
x
)
x
3
+
x
thỏa mãn F(1)0
F
(
x
)
x
4
a
+
x
2
b
-
3
c...
Đọc tiếp
F(x) là nguyên hàm của hàm số f ( x ) = x 3 + x thỏa mãn F(1)=0 F ( x ) = x 4 a + x 2 b - 3 c Tính S = a + b + c ?
A. 10
B. 12
C. 14
D. 16
Cho hàm số y f(x)
a
x
+
b
c
x
+
d
( a,b,c,d
∈
ℝ
,
-
d
c
≠
0) đồ thị hàm số y f’(x) như hình vẽ. Biết đồ thị hàm số y f(x) cắt...
Đọc tiếp
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.
Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.
Đúng 0
Bình luận (0)
Cho hàm số đa thức bậc ba yf(x) có đồ thị của các hàm số yf(x), yf (x)như hình vẽ bên.Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(f(x)-m)+2f(x)3(x+m) có đúng 3 nghiệm thực .Tổng các phần tử của S bằng A. 0 B. -6 C. -7 D. -5
Đọc tiếp
Cho hàm số đa thức bậc ba y=f(x) có đồ thị của các hàm số y=f(x), y=f '(x)như hình vẽ bên.Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(f(x)-m)+2f(x)=3(x+m) có đúng 3 nghiệm thực .Tổng các phần tử của S bằng
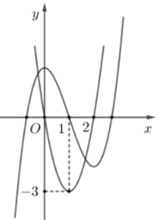
A. 0
B. -6
C. -7
D. -5
Ta có 
Quan sát đồ thị có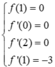 
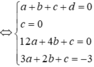
Đặt 
phương trình trở thành:
Khi đó 
Phương trình này có 3 nghiệm phân biệt
Tổng các phần tử củaS bằng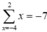 
Chọn đáp án C.
Đúng 0
Bình luận (0)
Kí hiệu F (x) là một nguyên hàm của hàm số
f
(
x
)
1
e
x
+
1
, biết
F
0
-
ln
2
. Tìm tập nghiệm S của phương trình
F
(
x
)
+
ln
(
e
x
+
1
)
3
. A.
S
-...
Đọc tiếp
Kí hiệu F (x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F 0 = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + ln ( e x + 1 ) = 3 .
A. S = - 3 ; 3
B. S = 3
C. S = ∅
D. S = - 3
Đáp án B
∫ 1 e x + 1 d x = ∫ d x - ∫ e x e x + 1 d x = x - ln ( e x + 1 ) + C
Vì F ( 0 ) = = - ln 2 ⇔ C = 0 ⇒ F ( x ) = x - ln e x + 1
Xét phương trình F ( x ) + ln ( e x + 1 ) = 3 ⇔ x = 3
Đúng 0
Bình luận (0)
Cho F(x)
1
2
x
2
là 1 nguyên hàm của hàm số
f
(
x
)
x
. Tìm nguyên hàm của hàm số f(x)lnx
Đọc tiếp
Cho F(x) = 1 2 x 2 là 1 nguyên hàm của hàm số f ( x ) x . Tìm nguyên hàm của hàm số f'(x)lnx
Cho
F
(
x
)
-
1
3
x
3
là một nguyên hàm của hàm số
f
(
x
)
x
Tìm nguyên hàm của hàm số f(x)lnx
Đọc tiếp
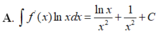
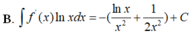
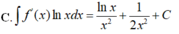
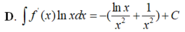
Cho F ( x ) = - 1 3 x 3 là một nguyên hàm của hàm số f ( x ) x Tìm nguyên hàm của hàm số f'(x)lnx
Cho hàm số y f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y f( x) trên [ a; e]? A.
m
a
x
[
a
,...
Đọc tiếp
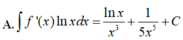
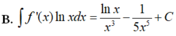
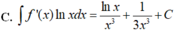
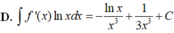
Cho hàm số y= f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f( x) trên [ a; e]?
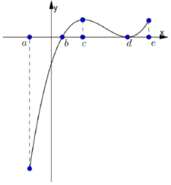
A. m a x [ a , e ] f ( x ) = f ( c ) m i n [ a , e ] f ( x ) = f ( a )
B. m a x [ a , e ] f ( x ) = f ( a ) m i n [ a , e ] f ( x ) = f ( b )
C. m a x [ a , e ] f ( x ) = f ( e ) m i n [ a , e ] f ( x ) = f ( b )
D. m a x [ a , e ] f ( x ) = f ( d ) m i n [ a , e ] f ( x ) = f ( b )
Ta có bảng biến thiên như hình vẽ sau:
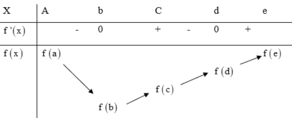
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.
Đúng 0
Bình luận (0)