Chọn 4 điểm thích hợp trên hình vẽ rồi nối để được:
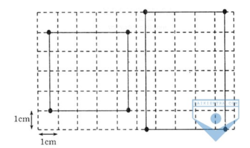
Cho hình chữ nhật ABCD. Chia mỗi cạnh AD và BC thành 4 phần bằng nhau, AB và CD thành 3 phần bằng nhau, rồi nối các điểm chia như hình vẽ. Ta đếm được bao nhiêu hình chữ nhật trên hình vẽ?
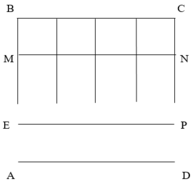
Trước hết Ta xét các hình chữ nhật tạo bởi hai đoạn AD, EP và các đoạn nối các điểm trên hai cạnh AD và BC. Bằng cách tương tự như tronh ví dụ 1 ta tính được 10 hình.
Tương tự ta tính được số hình chữ nhật tạo thành do hai đoạn EP và MN, do MN và BC đều bằng 10.
Tiếp theo ta tính số hình chữ nhật tạo thành do hai đoạn AD và MN, EP và BC với các đoạn nối các điểm trên hai cạnh AD và BC đều bằng 10.
Vì vậy :
Số hình chữ nhật đếm được trên hình vẽ là :
10 + 10 + 10 + 10 + 10 + 10 = 60 (hình)
Đáp số 60 hình.
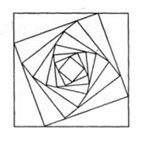
Một hình vuông \({C_1}\) có cạnh bằng 4. Người ta chia mỗi cạnh hình vuông thàng bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông \({C_2}\) (Hình 4). Từ hình vuông \({C_2}\) lại làm tiếp tục như trên để có hình vuông \({C_3}\). Cứ tiếp tục quá trình như trên, ta nhận được dãy các hình vuông \({C_1},{C_2},{C_3},..,{C_n},...\). Gọi \({a_n}\) là độ dài cạnh hình vuông \({C_n}\). Chứng minh rằng dãy số \(\left( {{a_n}} \right)\) là cấp số nhân.
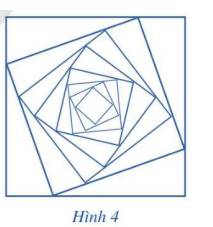
Ta có độ dài cạnh các hình vuông \({C_1},{C_2},{C_3},{C_4},...\;\) là \({a_1} = 4;{a_2} = \sqrt {10} ;{a_3} = \frac{5}{2};{a_4} = \frac{{5\sqrt {10} }}{8};...\)
Độ dài cạnh của hình vuông thứ n là: \({a_n} = \frac{{\sqrt {10} }}{4}{a_{n - 1}}\).
Vậy \(\frac{{{a_n}}}{{{a_{n - 1}}}} = \frac{{\sqrt {10} }}{4} = q\)
Vậy (an) là một cấp số nhân với số hạng đầu \({a_1} = 4\) và công bội \(q = \frac{{\sqrt {10} }}{4}\)
Để tô cạnh nối các điểm được đánh dấu bằng các số 3 và 4 trên hình bên, em thực hiện thao tác nào dưới đây?

A) Kéo thả chuột từ điểm 3 đến điểm 4
B) Nháy chuột
C) Nhấn một phím trên bàn phím
Hãy chọn thao tác đúng
Chọn cụm từ thích hợp rồi đặt vào chỗ trống để được câu hoàn chỉnh:
![]()
Tổng độ dài các cạnh của một hình tam giác là  của hình đó
của hình đó
Tổng độ dài các cạnh của hình tam giác là chu vi của hình đó.
Từ cần điền vào chỗ trống là “chu vi”
Cho hình vuông C 1 có cạnh bằng 4. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C 1 (hình bên). Từ hình vuông C 2 lại tiếp tục như trên để được hình vuông C 3 … Tiếp tục quá trình trên, ta nhận được các dãy các hình vuông C 1 , C 2 , C 3 , . . . , C n
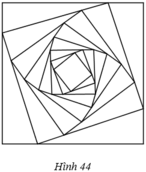
Gọi a n là độ dài cạnh của hình vuông C n . Chứng minh dãy số a n là một cấp số nhân.
Cạnh của hình vuông C1 là: a1 = 4 (giả thiết)
Giả sử cạnh hình vuông thứ n là an.
Theo định lý Py-ta-go : Cạnh hình vuông thứ n + 1 là :

⇒ (an) là cấp số nhân với a1 = 4 và công bội 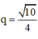
Cho hình vuông C 1 có cạnh bằng a. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C 2 (hình vẽ). Từ hình vuông C 2 lại tiếp tục làm như trên ta nhận được dãy các hình vuông C 1 , C 2 , C 3 , . . . C n . Gọi Si là diện tích của hình vuông C i ( i { 1 , 2 , 3 . . . } ) . Đặt T = S 1 + S 2 + . . . + S n biết rằng T=32/3, tính a?
A. 2
B. 5 2
C. 2
D. 2 2
Cho hình vuông C 1 có cạnh bằng a. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C 2 (hình vẽ). Từ hình vuông C 2 lại tiếp tục làm như trên ta nhận được dãy các hình vuông C 1 , C 2 , C 3 , . . . , C n . Gọi S i là diện tích của hình vuông C i i ∈ 1 ; 2 ; 3 ; . . . . . Đặt T = S 1 + S 2 + S 3 + . . . + S n + . . . biết rằng T = 32 3 , tính a?
A. 2
B. 5 2
C. 2
D. 2 2
Cho hình vuông C 1 có cạnh bằng a. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C 2 (hình vẽ). Từ hình vuông C 2 lại tiếp tục làm như trên ta nhận được dãy các hình vuông C 1 , C 2 , . . . C n . Gọi S i là diện tích của hình vuông C i ( i ∈ 1 , 2 , 3 . . . ) . Đặt T = S 1 + S 2 + . . . + S n + . . . biết rằng T=32/3, tính a
A. 2
A. 5 2
C. 2
D. 2 2
Một hình vuông C 1 cạnh bằng a. Chia mỗi cạnh hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để được hình vuông C 2 (như hình vẽ bên). Tiếp tục như thế ta được dãy các hình vuông C 1 , C 2 , C 3 ,... Gọi Si là diện tích của các hình vuông C i (i=1,2,...). Tìm a biết S 1 + S 2 + . . . + S n + . . . = 96 .

A. 3.
B. 6.
C. 9.
D. 4.