Chứng minh rằng trong 1 đường tròn, 2 cung bị chắn bởi 2 dây song song thì bằng nhau.

Những câu hỏi liên quan
Chứng minh rằng: trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
Vẽ đường tròn tâm O, các dây cung AB // CD.
Cần chứng minh 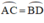
Cách 1:
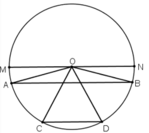
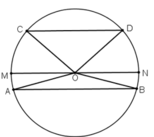
Kẻ bán kính MN // AB // CD
MN // AB

+ TH1: AB và CD cùng nằm trong một nửa đường tròn.
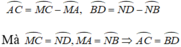 .
.
+ TH2: AB và CD thuộc hai nửa đường tròn khác nhau.
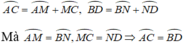
Cách 2:
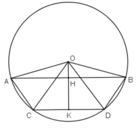
Kẻ OH ⊥ AB; OK ⊥ CD (H ∈ AB, K ∈ CD)
Vì AB // CD ⇒ O, H, K thẳng hàng.
ΔOAB có OA = OB
⇒ ΔOAB cân tại O
⇒ đường cao OH đồng thời là đường phân giác
⇒ 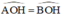
Chứng minh tương tự:
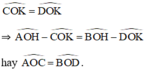
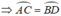
Đúng 0
Bình luận (0)
Chứng minh rằng: trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
Vẽ đường tròn tâm O, các dây cung AB // CD.
Cần chứng minh AC ^ = BD ^
Cách 1:
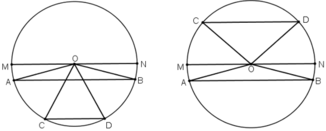
Kẻ bán kính MN // AB // CD
MN // AB

+ TH1: AB và CD cùng nằm trong một nửa đường tròn.
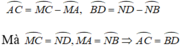 .
.
+ TH2: AB và CD thuộc hai nửa đường tròn khác nhau.
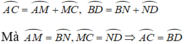
Cách 2:
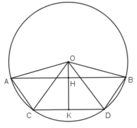
Kẻ OH ⊥ AB; OK ⊥ CD (H ∈ AB, K ∈ CD)
Vì AB // CD ⇒ O, H, K thẳng hàng.
ΔOAB có OA = OB
⇒ ΔOAB cân tại O
⇒ đường cao OH đồng thời là đường phân giác
⇒ 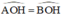
Chứng minh tương tự:
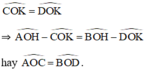
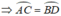
Kiến thức áp dụng
+ Trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau.
+ Trong cùng một đường tròn, hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau, tức là góc ở tâm chắn hai cung đó bằng nhau.
Đúng 0
Bình luận (0)
Chứng minh rằng trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
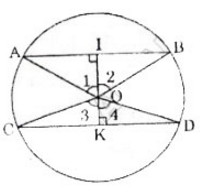
Giả sử AB và CD là các dây song song của đường tròn (O).
Kẻ OI ⊥ AB (I ∈ AB) và OK ⊥ CD (K∈CD).
Do AB //CD nên I,O,K thẳng hàng.
Do các tamgiác OAB, OCD là các tam giác cân đỉnh O nên các đường cao kẻ từ đỉnh đồng thời là phân giác.
Vì vậy ta có: Góc ∠O1 = ∠O2, ∠O3 = ∠O4
Giả sử AB nằm ngoài góc COD, ta có: ∠AOC = 1800 – (∠O1 + ∠O3) = 1800 -(∠O2 + ∠O4) = ∠BOD
Suy ra cung AC= cung BD.
Nghĩa là hai cung bị chắn giữa hai dây song song thì bằng nhau. Các trường hợp khác ta chứng minh tương tự.
Đúng 0
Bình luận (0)
Bài này có 2 TH, ta phải xét cả 2 TH (vì ko có ghi rõ đề):
TH 1:
Xét Δ
AOB có:
OA = OB (cùng bán kính)
Do đó: Δ
AOB cân tại A
⇒
ˆOAB=ˆOBA
Ta có: ˆAOM=ˆOBA
(2 góc so le trong do AB//MN)
ˆNOB=ˆOBA
( // )
mà ˆOAB=ˆOBA
(cmt)
⇒
ˆMOA=ˆNOB
(1)
CM tương tự, ta được: ˆMOC=ˆNOD
(2)
Từ (1) và (2) suy ra \(\widehat{AOC}=\widehat{BOD}\)
⇒ \(\widebat{AC}=\widebat{BD}\)
TH 2 :
CM y như câu a) (mà chỉ thay đổi cách CM \(\widehat{AOC}=\widehat{BOD}\) )
Đúng 0
Bình luận (0)
Chứng minh hai cung bị chắn bởi hai dây song song thì bằng nhau
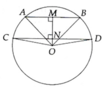
Trường hợp 1: Tâm O ở giữa của hai dây
Kẻ OM ⊥ AB, suy ra OM ⊥ CD tại N
Ta chứng minh được A O M ^ = B O M ^ (1)
Tương tự C O N ^ = D O N ^ (2)
Từ (1), (2) => A O C ^ = B O C ^ => A C ⏜ = B D ⏜
Trường hợp 2: Tâm O nằm ngoài khoảng hai dây
Kẻ OM ⊥ AB suy ra OM ⊥ CD tại N
Tương tự A O C ^ = B O C ^ => A C ⏜ = B D ⏜
Đúng 0
Bình luận (0)
Chứng minh rằng : Trong một đường tròn , hai cung bị chặn bởi hai dây song song thì bằng nhau .
Ai giúp mk vs :) tks
Kẻ \(OH\perp AB;OK\perp CD\left(H\in AB,K\in CD\right)\)
Vì AB // CD => O, H, K thẳng hàng.
Tam giác OAB có OA = OB
=> Tam giác OAB cân tại O
=> Đường cao OH đồng thời là đường phân giác
=> ^AOH = ^BOH
Chứng minh tương tự , ta có :
^COK = ^DOK
=> ^AOH - ^COK = ^BOH - ^DOK
hay ^AOC = ^BOD
\(\Rightarrow\widebat{AC}=\widebat{BD}\)
chứng minh định lý sau: Mỗi cặp đoạn thẳng song song bị chắn bởi 2 đường thẳng song song thì bằng nhau
Gọi giao điểm 4 đường thẳng lần lượt là A, B,C,D tạo thành 1 HCN ABCD
Nối B và C
Ta có góc C1= góc C2 (so le trong)
Xét tam giác ABC và tg BCD có:
góc C1 = góc C2
BC chung
=> tg ABC=tg BCD (ch-gn)
=> BD=AC(2 cạnh tương ứng
Đúng 0
Bình luận (0)
B1: Chứng minh rằng trong một đường tròn, hai dây cung không cắt nhau AB và CD là song song khi và chỉ khi hai cung AC và BD bằng nhau B2: Cho hai đường tròn tiếp xúc trong tại điểm A và BC là 1 dây của đường tròn lớn đường tiếp xúc với đường tròn nhỏ tại điểm D. Chứng minh rằng AD là phân giác của góc BAC
Mỗi câu sau đây đúng hay sai(A) Góc nội tiếp là góc tạo bởi hai dây của đường tròn đó.(B) Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.(C) Trong một đường tròn, hai góc nội tiếp không cùng chắn một cung thì không bằng nhau.(D) Trong một đường tròn, số đo của một góc nội tiếp bằng số đo cung bị chắn.(E) Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Đọc tiếp
Mỗi câu sau đây đúng hay sai
(A) Góc nội tiếp là góc tạo bởi hai dây của đường tròn đó.
(B) Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.
(C) Trong một đường tròn, hai góc nội tiếp không cùng chắn một cung thì không bằng nhau.
(D) Trong một đường tròn, số đo của một góc nội tiếp bằng số đo cung bị chắn.
(E) Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
(A) Sai. Góc nội tiếp là góc có đỉnh nằm trên đường tròn, hai cạnh chứa hai dây cung của đường tròn đó.
(B) Sai. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung hoặc chắn hai cung bằng nhau.
(C) Sai. Trong một đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau.
(D) Sai. Trong một đường tròn, số đo của góc nội tiếp bằng một nửa số đo của góc ở tâm cùng chắn một cung.
(E) Đúng. Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Đúng 0
Bình luận (0)
1,Chứng minh định lí : "Hai đoạn thẳng song song bị chắn giữa hai đường thẳng song song thì bằng nhau"
2,Chứng minhđịnh lí : "Trong tam giác vuông , trung tuyến tương ứng với cạnh huyền bằng nửa cạnh huyền"














