Bất phương trình mx - x - 3 ≤ m có nghiệm khi:
A . m ≤ 2 4
B . m ≥ 0
C . m < 2 4
D . m ≥ 2 4
Bất phương trình m x - x - 3 ≤ m có nghiệm khi:
A. m ≤ 2 4
B. m ≥ 0
C. m < 2 4
D. m ≥ 2 4
Cho bất phương trình 2 m 2 x + 10 − mx < 4 . Tìm m để bất phương trình có nghiệm x = − 3 .
Bất phương trình mx\(^2\)+2(m+3)x+m+1\(\ge\)0 vô nghiệm khi và chỉ khi
Cho hệ bất phương trình mx + 2 m > 0 2 x + 3 5 > 1 - 3 x 5
Xét các mệnh đề sau:
(I) Khi m< 0 thì hệ bất phương trình đã cho vô nghiệm.
(II) Khi m= 0 thì hệ bất phương trình đã cho có tập nghiệm là R
(III) Khi m≥ 0 thì hệ bất phương trình đã cho có tập nghiệm là 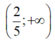
(IV) Khi m> 0 thì hệ bất phương trình đã cho có tập nghiệm là 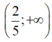
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
A. 1
B. 0
C. 2
D. 3
Cho hệ bất phương trình mx + 2 m > 0 2 x + 3 5 > 1 - 3 x 5
Xét các mệnh đề sau:
(I) Khi m< 0 thì hệ bất phương trình đã cho vô nghiệm.
(II) Khi m= 0 thì hệ bất phương trình đã cho có tập nghiệm là R.
(III) Khi m ≥ 0 thì hệ bất phương trình đã cho có tập nghiệm là 2 5 ; + ∞
(IV) Khi m > 0 thì hệ bất phương trình đã cho có tập nghiệm là 2 5 ; + ∞
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
A. 1
B. 0
C. 2
D. 3
Bất phương trình mx > 3 + m vô nghiệm khi:
A. m = 0
B. m > 0
C. m < 0
D. m ≠ 0
Chọn A.
Với m = 0, bất phương trình trở thành 0.x < 3 + 0 ⇒ 0 > 3 (vô lý)
Bất phương trình vô nghiệm khi m = 0.
Cho bất phương trình x − 1 3 + mx ≤ m − 9 . Tìm x để bất phương trình có nghiệm x = 10 .
Giá trị của m để bất phương trình m 2 x + 3 < mx + 4 có nghiệm là:
A. ∀x ∈ R
B. m = 0
C. m = 0 và m = 1
D. m = 1
Chọn A.
m
2
x + 3 < mx + 4 ⇔ m(m - 1)x < 1 vô nghiệm 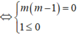 , vô lí.
, vô lí.
Vậy với ∀m ∈ R, bất phương trình có nghiệm.
Tìm m để bất phương trình \(\dfrac{x+1}{mx^2-4x+m-3}< 1\) có tập nghiệm là R
\(\Leftrightarrow\dfrac{mx^2-5x+m-4}{mx^2-4x+m-3}>0\)
BPT đã cho có tập nghiệm là R khi và chỉ khi:
\(\left\{{}\begin{matrix}\Delta_1=25-4m\left(m-4\right)< 0\\\Delta'_2=4-m\left(m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-4m^2+16m+25< 0\\-m^2+3m+4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< \dfrac{4-\sqrt{41}}{2}\\m>\dfrac{4+\sqrt{41}}{2}\end{matrix}\right.\)