Có bao nhiêu số nguyên m để tập nghiệm của bất phương trình 3 x + 2 - 3 3 x - m < 0 chứa đúng 10 số nguyên ?
A.![]()
B.![]()
C.![]()
D.![]()
Có bao nhiêu số nguyên m để tập nghiệm của bất phương trình 3 x + 2 - 3 3 x - m < 0 chứa đúng 10 số nguyên
A. 3 10 - 3 9
B. 3 9 - 3 8 - 1
C. 3 10 - 3 9 - 1
D. 3 9 - 3 8
Có ![]()
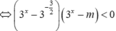
+) Nếu
m
≤
0
bất phương trình tương đương với  chứa vô số các số nguyên (loại);
chứa vô số các số nguyên (loại);
+) Nếu 0 < m < 3 - 3 2 không có số nguyên m nào cả (loại).
+) Nếu
m
>
3
-
3
2
bất phương trình tương đương với 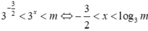
Tập nghiệm là ![]()
Vì S chứa đúng 10 số nguyên do đó ![]() ⇒
m
∈
3
8
+
1
,
.
.
.
,
3
9
Có tất cả
3
9
-
3
8
số nguyên thoả mãn.
⇒
m
∈
3
8
+
1
,
.
.
.
,
3
9
Có tất cả
3
9
-
3
8
số nguyên thoả mãn.
Chọn đáp án D.
Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình ( 3 x + 2 - 3 ) ( 3 x - 2 m ) < 0 chứa không quá 9 số nguyên?
A. 3281.
B. 3283.
C. 3280.
D. 3279.
Có bao nhiêu giá trị nguyên của tham số m để tập nghiệm của bất phương trình ln x 2 + 2 x + m - 2 ln ( 2 x - 1 ) > 0 chứa đúng hai số nguyên?
A. 10
B. 3
C. 4
D. 9
Cho bất phương trình 3 + x + 6 - x - 18 + 3 x - x 2 ≤ m 2 - m + 1 (m là tham số). Có bao nhiêu giá trị nguyên của m thuộc[-5;5] để bất phương trình nghiệm đúng với mọi x ∈ - 3 ; 6 ?
A. 3
B. 5
C. 9
D. 10
Đặt ![]()
Suy ra ![]()
Ta có ![]()
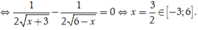
Ta có bảng biến thiên
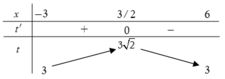
Từ bảng biến thiên ta suy ra ![]()
Khi đó bất phương trình trở thành: ![]()
![]()
Xét hàm số ![]() với
với ![]()
Ta có ![]()
Suy ra hàm số f(t) nghịch biến trên ![]()
![]()
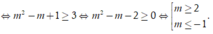
Chọn C.
tập nghiệm của bất phương trình \(2< \left|5-x\right|\le7\) có bao nhiêu số nguyên
Tập nghiệm của bất phương trình x 2 - 3 x + 1 + x - 2 ≤ 0 có tất cả bao nhiêu số nguyên?
A. Vô số
B. 4
C. 2
D. 3
Tập tập nghiệm của bất phương trình log 1 2 x + 2 ≥ - 2 có chứa bao nhiêu số nguyên
A. Vô số
B. 5
C. 4
D. 6
Có ![]()
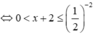
![]() có chứa tất cả 4 số nguyên.
có chứa tất cả 4 số nguyên.
Chọn đáp án C.
Có bao nhiêu nghiệm nguyên thuộc khoảng (-9;9) của tham số m để bất phương trình sau có nghiệm thực: 3 logx ≤ 2 log m x - x 2 - ( 1 - x ) 1 - x ?
A. 6.
B. 7.
C. 10.
D. 11.
Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình sau có nghiệm với mọi
x
∈
1
;
2
: ![]()
A. 3
B. 2
C. 1
D. 4