Tìm nghiệm của phương trình
1 + log 3 x 1 + log 9 x = 1 + log 27 x 1 + log 81 x
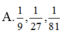
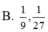
![]()
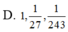
Tìm số nghiệm của phương trình x - 1 2 e x - 1 - log 2 = 0
A. 4
B. 3
C. 2
D. 0
Tìm tất cả các nghiệm của phương trình log x + log ( x - 9 ) = 1
A. {10}
B. {9}
C. {1;9}
D. {-1;10}
Tập nghiệm của bất phương trình log 2 x - 1 ≥ log x là
![]()
![]()
![]()
![]()
Tìm số nghiệm nguyên của bất phương trình log 5 2 3 x - 2 log 2 ( 4 - x ) - log ( 4 - x ) 2 + 1 > 0
A. 3
B. 1
C. 0
D. 2
Tìm số nghiệm nguyên của bất phương trình log 5 2 ( 3 x - 2 ) log 2 ( 4 - x ) - log ( 4 - x ) 2 + 1 > 0
A. 3
B. 1
C. 0
D. 2
Câu 11: Nghiệm của phương trình \(\log^2_{\frac{1}{2}} (x-2)-(2-x)\log_{2} (x-2)+3(x-5)=0\) là?
Tìm tập nghiệm của bất phương trình log ( x - 21 ) < 2 - log x
A. (-4; 25)
B. (0; 25)
C. (21; 25)
D. (25; +∞)
Cho phương trình: \(\left(x^2-1\right).log^2\left(x^2+1\right)-m\sqrt{2\left(x^2-1\right)}.log\left(x^2+1\right)+m+4=0\). Có bao nhiêu giá trị nguyên của tham số m thuộc [-10;10] để phương trình đã cho có 2 nghiệm phân biệt thỏa mãn \(1\le|x|\le3\)
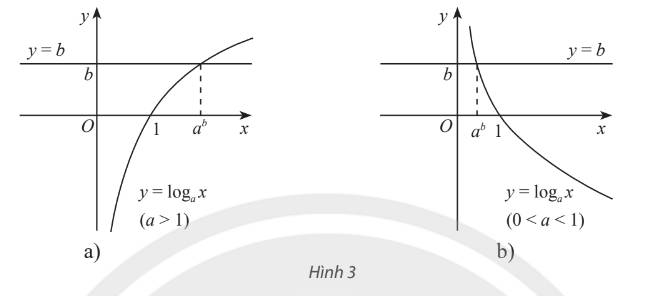
Cho đồ thị của hai hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) và \(y = b\) như Hình 3a (với \(a > 1\)) hay Hình 3b (với \(0 < a < 1\)). Từ đây hãy nhận xét về số nghiệm và công thức nghiệm của phương trình \({\log _a}x = b\).
tham khảo.
Đồ thị của hai hàm số \(y=\log_ax\) và \(y=b\) luôn cắt nhau tại một điểm duy nhất. Khi đó phương trình \(\log_ax=b\) có nghiệm duy nhất \(x=a^b\).
Tập nghiệm của phương trình log x 2 - 2 x + 2 = 1 là
A. ∅
B. - 2 ; 4
C. 4
D. - 2