Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Tính thể tích V của khối tứ diện ABCD
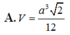
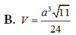
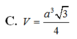
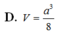
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Tính thể tích V của khối tứ diện ABCD
A. V = a 3 2 12
B. V = a 3 11 24
C. V = a 3 3 4
D. V = a 3 8
Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng
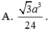
![]()
![]()
![]()
Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng
A. 3 a 3 24 .
B. 2 π a 3 24 .
C. 2 2 a 3 9 .
D. 3 π a 3 8 .
Đáp án B
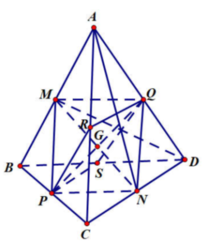
Gọi G là trọng tâm tứ diện ABCD. Ta chứng minh G là tâm mặt cầu tiếp xúc với tất cả các cạnh của tứ diện.
Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, CD, BC, AD, AC, BD.
Ta có G là trung điểm của các đoạn MN, PQ, RS.
Δ A C D = Δ B C D ⇒ A N = B N ⇒ Δ N A B cân tại N ⇒ M N ⊥ A B
Tương tụ ta có M N ⊥ C D .
Ta có: P Q = R S = M N = A N 2 − A M 2 = a 3 2 2 − a 2 4 = a 2 2 .
Suy ra d G , A B = d G , C D = 1 2 M N = a 2 4 .
Chứng minh tương tự ta có d G , A C = d G , A D = d G , B D = d G , B C = a 2 4
Vậy G là tâm mặt cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD.
Bán kính mặt cầu R = a 2 4 . Suy ra thể tích khối cầu là V = 4 3 π R 3 = 4 3 π a 2 4 3 = 2 π a 3 24 .
Tính thể tích V của khối cầu tiếp xúc với tất cả các cạnh của tứ diện đều ABCD cạnh bằng 1.
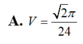
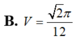
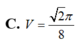
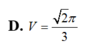
Tính thể tích V của khối cầu tiếp xúc với tất cả các cạnh của tứ diện đều ABCD cạnh bằng 1.
A. V = 2 π 24
B. V = 2 π 12
C. V = 2 π 8
D. V = 2 π 3
Đáp án A
Phương pháp: Xác định tâm mặt cầu ngoại tiếp khối chóp tam giác đều.
B1: Xác định hai trục của hai mặt phẳng bất kì (đường thẳng đi qua tâm đường tròn ngoại tiếp đáy và vuông góc với đáy).
B2: Xác định giao điểm I của hai trục đó. Khi đó I là tâm mặt cầu cần tìm.
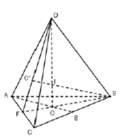
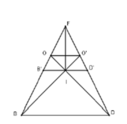
Cách giải: Gọi O và O’ lần lượt là tâm tam giác đều ABC và ACD thì D O ⊥ A B C ; B O ' ⊥ A C D
Gọi I = D O ∩ B O ' , ta dễ dạng chứng minh được I là tâm mặt cầu tiếp xúc với các cạnh của tứ diện đều.
Và R = IF là bán kính mặt cầu đó.
Kẻ BB’ qua I và song song với BD.
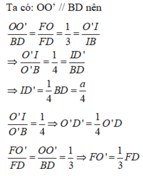
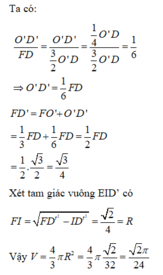
Cho khối tứ diện ABCD có thể tích bằng V, thể tích của khối đa diện có đỉnh là trung điểm các cạnh của tứ diện ABCD bằng V'. Tính tỉ số V'/V.
A. V ' V = 1 2
B. V ' V = 1 8
C. V ' V = 1 4
D. V ' V = 3 4
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng 60 O . Tính thể tích V của khối tứ diện ABCD theo a:
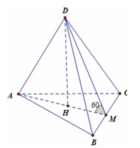
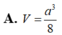
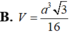
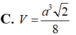
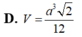
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng 60 ° . Tính thể tích V của khối tứ diện ABCD theo a:
A. V = a 3 8
B. V = a 3 3 16
C. V = a 3 2 8
D. V = a 3 2 12
Đáp án B
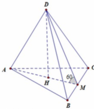
Gọi M là trung điểm của BC khi đó D M ⊥ B C A M ⊥ B C
Suy ra B C ⊥ ( D M A ) ⇒ D B C ; A B C ^ = 60 °
Lại có D M = A M = a 3 2
Dựng D H ⊥ A M ⇒ D H ⊥ ( A B C )
Khi đó V A B C D = 1 3 D H . S A B C = 1 3 D M . sin 60 ° . a 2 3 4 = a 2 3 16 .
Cho khối tứ diện ABCD có thể tích bằng V, thể tích của khối đa diện có đỉnh là trung điểm các cạnh của tứ diện ABCD bằng V' Tính tỉ số V ' V .
A. V ' V = 1 2
B. V ' V = 1 8
C. V ' V = 1 4
D. V ' V = 3 4