Cho tam giác ABC vuông tại A có BC = 12cm . B = 60 ° . a ) Giải tam giác ABC . b ) Tính đường cao AH của MBC .

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AC=12cm; BC=15cm
a) Giải tam giác vuông ABC
b) Tính độ dài đường cao AH và đường phân giác AD của tam giác ABC
a, Cho tam giác ABC vuông tại A có AB =3/5 BC . Đường cao AH =12cm . Tính chu vi tam giác ABC .
b, Cho tam giác ABC vuông tại A có đường cao AH , phân giác AD . Biết BD=15cm ,DC=20cm.Tính AH,AD
GIÚP MIK . THANKS
a, Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow BC^2=\left(\frac{3}{5}BC\right)^2+AC^2\)
\(\Leftrightarrow AC^2=\frac{16}{25}BC^2\Leftrightarrow AC=\frac{4}{5}BC\)
* Áp dụng hệ thức :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{144}=\frac{1}{\frac{9}{25}BC^2}+\frac{1}{\frac{16}{25}BC^2}\)
\(\Leftrightarrow\frac{1}{144}=\frac{\frac{16}{25}BC^2+\frac{9}{25}BC^2}{\frac{16}{25}BC^2.\frac{9}{25}BC^2}\Rightarrow144BC^2=\frac{144}{625}BC^4\)
\(\Leftrightarrow\frac{144}{625}BC^2-144=0\Leftrightarrow BC^2=144.\frac{625}{144}=625\Leftrightarrow BC=25\)cm
\(\Rightarrow AB=\frac{3}{5}BC=\frac{3}{5}.25=\frac{75}{5}=15\)cm
\(\Rightarrow AC=\frac{4}{5}BC=\frac{4}{5}.25=\frac{100}{5}=20\)
Chu vi tam giác là : \(P_{ABC}=AB+BC+AB=15+20+25=60\)cm2
b, Vì AD là phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}=\frac{15}{20}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\)
Lại có : \(BC=BD+DC=15+20=35\)cm
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(BC^2=AC^2+AB^2=AC^2+\left(\frac{3}{4}AC\right)^2\)
\(\Rightarrow\frac{25}{16}AC^2=1225\Leftrightarrow AC^2=\frac{16.1225}{25}=784\Leftrightarrow AC=28\)cm
\(\Rightarrow AB=\frac{3}{4}.28=21\)cm
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{AH^2}=\frac{AC^2+AB^2}{AB^2AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{784+441}{345744}\Leftrightarrow1225AH^2=345744\Leftrightarrow AH^2=\frac{7056}{25}\Leftrightarrow AH=\frac{84}{5}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{441}{35}=\frac{63}{5}\)cm
\(\Rightarrow HD=BD-BH=15-\frac{63}{5}=\frac{12}{5}\)cm
Áp dụng định lí Pytago cho tam giác AHD vuông tại H
\(AD^2=AH^2+HD^2=\left(\frac{84}{5}\right)^2+\left(\frac{12}{5}\right)^2=288\Rightarrow AD=12\sqrt{2}\)cm
Cho tam giác ABC vuông tại A, AB = 5cm, AC = 12cm, đường cao AH. a) Tính BC, BH, AH. b) Gọi AM là đường trung tuyến của tam giác ABC, tính diện tích tam giác AHM
\(a,BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\\ HTL:\left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=\dfrac{60}{13}\left(cm\right)\\BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\end{matrix}\right.\\ b,AM=\dfrac{1}{2}BC=\dfrac{13}{2}\left(cm\right)\left(trung.tuyến.ứng.cạnh.huyền\right)\\ \Rightarrow HM=\sqrt{AM^2-AH^2}=\dfrac{119}{26}\left(cm\right)\\ \Rightarrow S_{AHM}=\dfrac{1}{2}AH\cdot HM=\dfrac{1}{2}\cdot\dfrac{60}{13}\cdot\dfrac{119}{26}=\dfrac{1785}{169}\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A Có cạnh AC = 12cm cạnh BC = 15cm . hãy giải tam giác ABC
b . tính độ dài đường cao AH và độ dài đường phân giác thuộc góc A
ta có \(\sin B=\frac{AC}{BC}=\frac{12}{15}=\frac{4}{5}\Rightarrow\widehat{B}\approx53^o\)
\(\Rightarrow\widehat{C}=90^o-\widehat{B}\approx37^o\)
... Py-ta-go \(\Rightarrow AB^2=BC^2-AC^2=15^2-12^2=9^2\)
\(\Rightarrow AB=9cm\)
b, gọi BD là x .Áp dụng tc đường phân giác ta có:
\(\frac{AB}{AC}=\frac{BD}{CD}=\frac{x}{BC-x}\)(x<15)
\(\Rightarrow\frac{9}{12}=\frac{x}{15-x}\Rightarrow x=\frac{45}{7}cm\)
Hệ thức lượng \(\Rightarrow AB.AC=BC.AH\Rightarrow AH=\frac{AC.AB}{BC}\)\(\Rightarrow AH=\frac{9.12}{15}=7,2\left(cm\right)\)
.... Py-ta-go: \(\Rightarrow BH^2=AB^2-AH^2=9^2-7,2^2=29,16\)
\(\Rightarrow BH=5,4cm\)
do AB<AC nên H nằm giữa B và D
\(\Rightarrow HD=BD-BH=\frac{45}{7}-5,4=\frac{36}{35}\left(cm\right)\)
... py ta go..\(AD^2=HD^2+AH^2=\left(\frac{36}{35}\right)^2+7,2^2\)
\(\Rightarrow AD^2=\frac{2592}{49}\Rightarrow AD=\frac{36\sqrt{2}}{7}cm\)
Bạn tự kết luận nha! hồi nãy mk đã gửi một bài chi tiết hết sức rồi mà olm lại báo có lỗi xảy ra nên ko gửi lên được!
Mấy cái chỗ .... thì bạn tự điền thêm vào nha!
k cho mk là được rồi! mk ko cần thẻ! cám ơn!
Đúng 2
Bình luận (0)
ta có \(\sin B=\frac{AC}{BC}=\frac{12}{15}=\frac{4}{5}\Rightarrow\widehat{B}\approx53^o\)
\(\Rightarrow\widehat{C}=90^o-\widehat{B}\approx37^o\)
... Py-ta-go \(\Rightarrow AB^2=BC^2-AC^2=15^2-12^2=9^2\)
\(\Rightarrow AB=9cm\)
b, gọi BD là x .Áp dụng tc đường phân giác ta có:
\(\frac{AB}{AC}=\frac{BD}{CD}=\frac{x}{BC-x}\)(x<15)
\(\Rightarrow\frac{9}{12}=\frac{x}{15-x}\Rightarrow x=\frac{45}{7}cm\)
Hệ thức lượng \(\Rightarrow AB.AC=BC.AH\Rightarrow AH=\frac{AC.AB}{BC}\)\(\Rightarrow AH=\frac{9.12}{15}=7,2\left(cm\right)\)
.... Py-ta-go: \(\Rightarrow BH^2=AB^2-AH^2=9^2-7,2^2=29,16\)
\(\Rightarrow BH=5,4cm\)
do AB<AC nên H nằm giữa B và D
\(\Rightarrow HD=BD-BH=\frac{45}{7}-5,4=\frac{36}{35}\left(cm\right)\)
... py ta go..\(AD^2=HD^2+AH^2=\left(\frac{36}{35}\right)^2+7,2^2\)
\(\Rightarrow AD^2=\frac{2592}{49}\Rightarrow AD=\frac{36\sqrt{2}}{7}cm\)
Bạn tự kết luận nha! hồi nãy mk đã gửi một bài chi tiết hết sức rồi mà olm lại báo có lỗi xảy ra nên ko gửi lên được!
Lần 2 nó lại bảo phải kiểm duyệt trước khi hiển thị! Ức chế hết sức!!! chương trình này có lẽ lỗi nặng?
Mấy cái chỗ .... thì bạn tự điền thêm vào nha!
k cho mk là được rồi! mk ko cần thẻ! cám ơn!
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.
a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.
b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào?
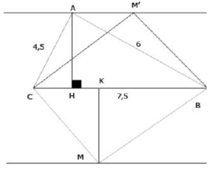
a) Ta có: A B 2 + A C 2 = 6 2 + 4 , 5 2 = 7 , 5 2 = B C 2
nên tam giác ABC vuông tại A. (đpcm)
![]()
= > ∠ B = 37 ° = > ∠ C = 90 ° - ∠ B = 90 ° - 37 ° = 53 °
Mặt khác trong tam giác ABC vuông tại A, ta có:
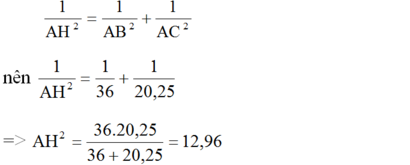
=> AH = 3,6 cm
b) Gọi khoảng cách từ M đến BC là MK. Ta có:
![]()
Ta thấy SMBC = SABC khi MK = AH = 3,6 cm
Do đó để SMBC = SABC thì M phải nằm trên đường thẳng song song và cách BC một khoảng là 3,6 cm (có hai đường thẳng như trên hình).
Đúng 0
Bình luận (0)
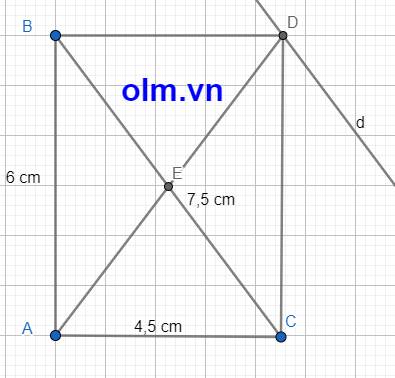
cho tam giác ABC có AB=6cm, AC=4,5cm, BC=7,5cm.
a)Chứng minh tam giác ABC vuông tại A. Tính các góc B,C và đường cao AH của tam giác đó.
b)Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào?
a, Xét \(\Delta\)ABC có: AB2 + AC2 = 62 + 4,52 = 56,25 (cm2)
BC2 = 7,52 = 56,25 (cm2)
AB2 + AC2 = BC2 vậy tam giác ABC vuông tại A (đpcm)
SinC = 6 : 7,5 =0,8 ⇒ \(\widehat{C}\) = 53,130 ⇒ \(\widehat{B}\) = 900 - 53,130 = 36,870
b, Dựng hình chữ nhật ABCD, chiều cao AH, DK, và đường thẳng d đi qua D song song với BC như hình vẽ ta có
SABC = SBDC ⇒ AH = DK
Lây 1 điểm bất M kỳ di động trên đường thẳng d ta có:
SBDC = SMBC (vì hai tam giác có chiều cao bằng nhau và chung cạnh đáy BC)
⇒ SABC = SMBC
Kết luận khi M di động trên đường thẳng d thì diện tích tam giác MBC luôn bằng diện tích tam giác ABC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 12cm, AC =16cm. Vẽ đường cao AH.
a) Cm tam giác HBA đồng dạng tam giác ABC.
b) Tính BC,AH,BH.
c)Vẽ đường phân giác AD của tam giác ABC( D thuộc BC).Tính BD,CD
Tự vẽ hình nha
a) xét tam giác HAB và tam giác ABC
góc AHB = góc ABC
góc CAB : chung
Suy ra : tam giác AHB ~ tam giác ABC ( g-g )
b) Áp dụng định lí py - ta - go vào tam giác ABC ta được :
AC2 + AB2 = BC2
162 + 122 = BC2
400 = BC2
=> BC = \(\sqrt{400}\)= 20 ( cm )
ta có tam giác HAB ~ tam giác ABC ( câu a )
=> \(\frac{AH}{AC}=\frac{AB}{BC}hay\frac{AH}{16}=\frac{12}{20}\)
=> AH = \(\frac{12.16}{20}=9,6\)( cm )
Độ dài cạnh BH là
Áp dụng định lí py - ta - go vào tam giác HBA ta được :
AH2 + BH2 = AB2
BH2 = AB2 - AH2
BH2 = 122 - 9,62
BH2 = 51,84
=> BH = \(\sqrt{51,84}\) = 7,2 ( cm )
c) Vì AD là đường phân giác của tam giác ABC nên :
\(\frac{AB}{BD}=\frac{AC}{CD}\Leftrightarrow\frac{AB}{BC-CD}=\frac{AC}{CD}\)
<=> \(\frac{AB.CD}{CD\left(BC-CD\right)}=\frac{AC\left(BC-CD\right)}{CD\left(BC-CD\right)}\)
<=> AB.CD = AC(BC - CD)
hay 12CD = 16.20 - 16CD
<=> 12CD+ 16CD = 320
<=> 28CD = 320
<=> CD = \(\frac{320}{28}\approx11.43\left(cm\right)\)
Độ dài cạnh BD là :
BD = BC - CD
BD = 20 - \(\frac{320}{28}\)\(\approx\) 8,57 ( cm )
Đúng 0
Bình luận (0)
Cho hỏi đồng dạng là sao bạn???Tớ mới học lớp 7 thôi,nên chưa biết ^^
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A. Biết AB=9cm, AC=12cm. Vẽ AH là đường cao của tam giác ABC a) tính độ dài BC b) chứng minh tam giác ABC s tam giác HBA
a: BC=15cm
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
Đúng 0
Bình luận (0)
a.
Vì ΔABC vuông tại A nên theo định lí Py - ta - go:
BC2 = AB2 + AC2
BC2 = 92 + 122
\(\Rightarrow\) BC2 = 225
\(\Rightarrow\) BC2 = \(\sqrt{225}\) = 15 cm
b. Xét ΔABC và Δ HBA:
\(\widehat{A}=\widehat{H}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) ΔABC \(\sim\) Δ HBA (g.g)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB =12cm , AC=16cm . Vẽ đường cao AH a, chứng minh tam giác HBA đồng dang với tam giác ABC b, Tính BC,BH c, tính diện tích tam giác ABC
a: Xet ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng vơi ΔABC
b: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
BH=12^2/20=7,2cm
c: \(S_{ABC}=\dfrac{1}{2}\cdot12\cdot16=6\cdot16=96\left(cm^2\right)\)
Đúng 0
Bình luận (0)
























