Tìm các giá trị a ∈ ℝ để (C): y = ( x - 1 ) 2 ( a - x ) có một tiếp tuyến chính là trục hoành.
![]()
![]()
![]()
![]()
Tìm các giá trị của m(m ∈ ℝ ) để y = x + m x 2 + 1 có cực đại
![]()
![]()
![]()
![]()
Tìm các giá trị m ∈ ℝ để hàm số: y = x - m x 2 + 1 có cực đại


![]()
![]()
Tìm các giá trị m ∈ ℝ để x 4 + 4 m x 3 + 27 ≥ 0 , ∀ x ∈ ℝ .
![]()
![]()
![]()
Tìm các giá trị của tham số m để hàm số y = m sin x + 7 x - 5 m + 3 có y ' ≥ 0 , ∀ x ∈ ℝ .
A. - 7 ≤ m ≤ 7
B. m ≤ 1
C. m ≥ 7
D. m ≤ - 7
Tìm các giá trị a ∈ ℝ để phương trình log 3 3 - x = a có nghiệm.
A. a ≥ 0
B. b ≤ a ≤ 1
C. a ≤ 1
D. ∀ a ∈ ℝ
Tìm tất cả các giá trị của để hàm số y = x + m ( sin x + cos x ) đồng biến trên ℝ
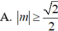
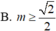
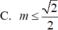
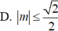
Tìm tất cả các giá trị của tham số m để hàm số y = x + m x 2 + x + 1 có giá trị lớn nhất trên ℝ nhỏ hơn hoặc bằng 1.
A. m ≤ 1
B. m ≥ 1
C. m ≥ -1
D. m ≤ -1
Chọn A.
TXĐ: D = R.
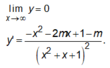
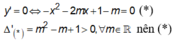 có 2 nghiệm phân biệt
có 2 nghiệm phân biệt ![]()
BBT:
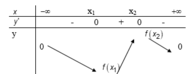
Vậy hàm số đạt giá trị lớn nhất là
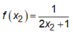
![]()
YCBT 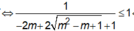
![]()
![]()
![]()
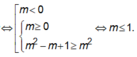
Tìm tất cả các giá trị của tham số m để hàm số y = x + m x 2 + x + 1 có giá trị lớn nhất trên ℝ nhỏ hơn hoặc bằng 1.
A. m ≤ 1
B. m ≥ 1
C. m ≥ - 1
D. m ≤ - 1
Cho hàm số y = f x có f ' x > 0, ∀ x ∈ ℝ . Tìm tập tất cả các giá trị thực của x để f 1 x < f 1 .
A. − ∞ ; 0 ∪ 0 ; 1
B. 0 ; 1
C. 1 ; + ∞
D. − ∞ ; 1
Đáp án C
Theo giả thiết f ' x > 0, ∀ x ∈ R , do đó f 1 x < f 1 ⇔ 1 x < 1 ⇔ x > 1
Suy ra với x ∈ 1, + ∞ thì f 1 x < f 1 . Chọn phương án C.