Các câu hỏi tương tự
Tìm các giá trị
m
∈
ℝ
để hàm số:
y
x
-
m
x
2
+
1
có cực đại
Đọc tiếp
Tìm các giá trị m ∈ ℝ để hàm số: y = x - m x 2 + 1 có cực đại


![]()
![]()
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Tìm các giá trị của tham số m để đồ thị hàm số y =mx^4 +(2m-1)x^2 +m -2 chỉ có 1 cực đại và ko có cực tiểu.
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
+
(
m
-
1
)
x
+
2
có cực đại, cực tiểu và các đ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + ( m - 1 ) x + 2 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
A. 0 ≤ m ≤ 1
B. m ≥ 1
C. m ≥ 0
D. m > 1
Tìm các giá trị thực của m để hàm số
y
x
+
m
x
2
+
1
có cực đại.
Đọc tiếp
Tìm các giá trị thực của m để hàm số y = x + m x 2 + 1 có cực đại.
![]()
![]()
![]()
![]()
Cho (C): y=(x+1)(x-2)(x-m). Xác định m ∈ ℝ để (C) có cực đại, cực tiểu
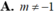
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số
m
để hàm số
y
1
3
x
3
-
m
x
2
+
(
m
+
1
)
x...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 - m x 2 + ( m + 1 ) x - 1 đạt cực đại tại x = - 2 ?
A. Không tồn tại m
B. -1
C. 2
D. 3
Tìm tất cả các giá trị thực của tham số m để hàm số:
y
1
3
x
3
+
m
x
2
+
(
m
+
6
)
x
+
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số: y = 1 3 x 3 + m x 2 + ( m + 6 ) x + m có cực đại và cực tiểu
A. -2 < m < 3
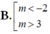
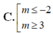
D. - 2 ≤ m ≤ 3 .
Tìm các giá trị của
m
∈
ℝ
để đồ thị hàm số
y
m
x
4
-
(
m
2
-
1
)
x
2
-
1
chỉ có một điểm cực trị và đó là cực tiểu.
Đọc tiếp
Tìm các giá trị của m ∈ ℝ để đồ thị hàm số y = m x 4 - ( m 2 - 1 ) x 2 - 1 chỉ có một điểm cực trị và đó là cực tiểu.
![]()
![]()
![]()
![]()





