- Với \(m=0\Rightarrow y=-x^2-2\) chỉ có cực đại (thỏa mãn)
- Với \(m\ne0\) hàm chỉ có cực đại khi:
\(\left\{{}\begin{matrix}m< 0\\m\left(2m-1\right)\ge0\end{matrix}\right.\) \(\Leftrightarrow m< 0\)
Vậy \(m\le0\)
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 3 - 3 x 2 - m x + 2 có điểm cực đại và điểm cực tiểu cách đều đường thẳng có phương trình: y = x - 1 ( d )
A. m = 0
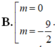
C. m = 2
D. m = - 9 2
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + ( m - 1 ) x + 2 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
A. 0 ≤ m ≤ 1
B. m ≥ 1
C. m ≥ 0
D. m > 1
Tìm các giá trị của tham số m để đồ thị hàm số: y = 2 x 3 + 3 ( m - 1 ) x 2 + 6 m ( 1 - 2 m ) x có điểm cực đại và điểm cực tiểu nằm trên đường thẳng có phương trình: y = - 4 x ( d )
A. m ∈ 1
B. m ∈ 0 ; 1
C. m ∈ 0 ; 1 2 ; 1
D. m ∈ 1 2
Cho hàm số y = (m + 2)x3 + 3x2 + mx - 5, m là tham số. Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương
A. 
B.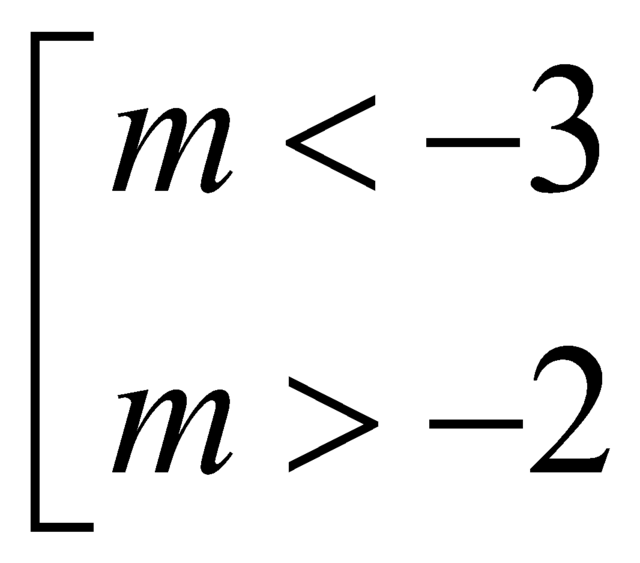 
C. 
D. 
Cho hàm số y = x 4 - 2 ( 1 - m 2 ) x 2 + m + 1 . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất
A. m = - 1 2
B. m = 1 2
C. m = 0
D. m = 1
Cho hàm số y=x3+3x2+mx+m-2 với m là tham số thực, có đồ thị là (C) . Tìm tất cả các giá trị của m để (C) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành.
A. m<2
B. m ≤ 3
C. m<3
D. m ≤ 2 .
Tìm tất cả các giá trị của m để đồ thị hàm số y = ( m 2 - 1 ) x 4 + m x 2 + m - 2 chỉ có một điểm cực đại và không có điểm cực tiểu.
A. -1,5 < m ≤ 0
B. m ≤ 1
C. -1 ≤ m ≤ 0
D. -1 < m < 0,5
Tìm tất cả các giá trị thực của tham số m để điểm M( 2m3; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y= 2x3-3( 2m+ 1) x2+ 6m( m+1) x+1 (C) một tam giác có diện tích nhỏ nhất.
A. -1
B. 0
C. 1
D. 2
Tìm tất cả các giá trị thực của tham số m để điểm M ( 2 m 3 ; m ) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y = 2 x 3 - 3 ( 2 m + 1 ) x 2 + 6 m ( m + 1 ) x + 1 một tam giác có diện tích nhỏ nhất
A. m = 2
B. m = 0
C. m = 1
D. m = -1
