Hàm số y = log a x v à y = log b x có đồ thị như hình vẽ bên:
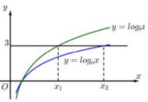
Đường thẳng y = 3 cắt hai đồ thị tại các điểm có hoành độ .
Biết rằng x 2 = 2 x 1 , giá trị a b của bằng:
A. 1 2
B. 3
C. 2
D. 2 3
Trong các hàm số sau, những hàm số nào là hàm số lôgarit? Khi đó hãy chỉ ra cơ số.
a) \(y = {\log _{\sqrt 3 }}x;\)
b) \(y = {\log _{{2^{ - 2}}}}x;\)
c) \(y = {\log _x}2;\)
d) \(y = {\log _{\frac{1}{x}}}5.\)
Hàm số a,b là các hàm số logarit
a: \(log_{\sqrt{3}}x\)
Cơ số là \(\sqrt{3}\)
b: \(log_{2^{-2}}x\)
Cơ số là \(2^{-2}=\dfrac{1}{4}\)
Cho đồ thị ba hàm số \(y = {\log _a}x,y = {\log _b}x\) và \(y = {\log _c}x\) như hình bên. Mệnh đề nào sau đây là đúng?
A. \(a > b > c\).
B. \(b > a > c\).
C. \(a > b > c\).
D. \(b > c > a\).
Hàm số \(y=log_cx\) nghịch biến
\(\Rightarrow0< c< 1\) và các hàm \(y=log_ax,y=log_bx\) đồng biến nên \(a,b>1\)
Ta chọn \(x=100\Rightarrow log_a>log_b100\Rightarrow a< b\Rightarrow b>a>c\)
\(\Rightarrow B\)
\(log_cx\) nghịch biến biến nên 0<c<1
\(log_ax;log_bx\) đồng biến nên a>1; b>1
=>Loại D
\(log_ax>log_bx\left(x>1\right)\)
=>\(\dfrac{1}{log_xa}< \dfrac{1}{log_xb}\)
=>a<b
=>Chọn B
Vẽ đồ thị của các hàm số sau:
a) \(y = \log x;\)
b) \(y = {\log _{\frac{1}{3}}}x.\)
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit \(y = {\log _a}x;\,y = {\log _b}x;\,y = {\log _c}x\) được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?
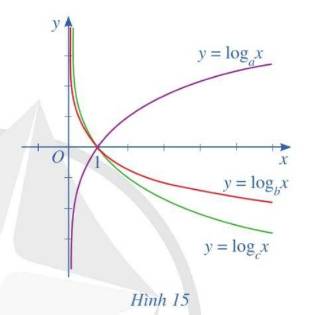
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
Cho bốn số thực dương a, b, x, y với \(a,b \ne 1\). Khẳng định nào sau đây là sai?
A. \({\log _a}(xy) = {\log _a}x + {\log _b}y\).
B. \({\log _a}\frac{x}{y} = {\log _a}x - {\log _a}y\).
C. \({\log _a}\frac{1}{x} = \frac{1}{{{{\log }_a}x}}\).
D. \({\log _a}b \cdot {\log _b}x = {\log _a}x\).
Vẽ đồ thị các hàm số:
a) \(y = \log x\);
b) \(y = {\log _{\frac{1}{4}}}x\).
Cho đồ thị của hàm số \(y = {\log _2}x\) và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {\log _2}x\) nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình \({\log _2}x > 2.\)

Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)
Tìm tập xác định của các hàm số sau :
a) \(y=\dfrac{2}{\sqrt{4^x-2}}\)
b) \(y=\log_6\dfrac{3x+2}{1-x}\)
c) \(y=\sqrt{\log x+\log\left(x+2\right)}\)
d) \(y=\sqrt{\log\left(x-1\right)+\log\left(x+1\right)}\)
Tính đạo hàm của các hàm số sau:
a) \(y = x{\log _2}x\);
b) \(y = {x^3}{e^x}\).
a: \(y'=\left(x\cdot log_2x\right)'=log_2x+x\cdot\dfrac{1}{x\cdot ln2}=log_2x+\dfrac{1}{ln2}\)
b: \(y'=\left(x^3e^x\right)'=\left(x^3\right)'\cdot e^x+x^3\cdot\left(e^x\right)'\)
\(=3x^2\cdot e^x+x^3\cdot e^x\)
Đề bài
Hàm số nào sau đây nghịch biến trên tập xác định của nó?
A. \(y = {\log _3}x\)
B. \(y = {\log _{\sqrt 3 }}x\)
C. \({\log _{\frac{1}{e}}}x\)
D. \(y = {\log _\pi }x\)
Vì \(\dfrac{1}{e}\simeq0,368< 1\)
\(\Rightarrow y=log_{\dfrac{1}{e}}\left(x\right)\) nghịch biến trên D = \(\left(0;+\infty\right)\)
Chọn C.
0<1/e<1
=>\(log_{\dfrac{1}{e}}\left(x\right)\) nghịch biến
=>C