Trong không gian tọa độ Oxyz, cho tứ diện ABCD có A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;-1). Thể tích của tứ diện ABCD bằng
A. 1
B. 2
C. 1 2
D. 1 3
Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Chọn D.
Gọi G(a,b,c) là trọng tâm của tứ diện, ta có:
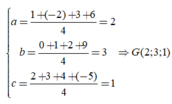
Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Chọn D.
Gọi G(a,b,c) là trọng tâm của tứ diện, ta có:
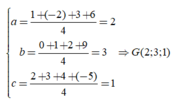
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A, B, C,D. Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ là:
A. (3/2;-3/2;3/2)
B. (3/2;3/2;3/2)
C. (-3/2;3/2;3/2)
D. (3/2;3/2;-3/2)
Trong không gian với hệ tọa độ Oxyz cho tứ diện ABCD với A 2 ; 1 ; - 1 , B 3 ; 0 ; 1 , C 2 ; - 1 ; 3 , điểm D thuộc Oy và thể tích của tứ diện ABCD bằng 5. Tọa độ của đỉnh D là
A. D(0;-7;0)
B. D(0;8;0)
C. D(0;-7;0) hoặc D(0;8;0)
D. D(0;7;0) hoặc D(0;-8;0)
Trong không gian tọa độ Oxyz, cho tứ diện ABCD với A(-1;-2;4), B(-4;-2;0), C(3;-2;1) và D(1;1;1) . Độ cao của tứ diện kẻ từ D bằng
A. 3.
B. 1.
C. 2.
D. 0,5
Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD với A 0 ; 1 ; 1 , B 0 ; 2 ; 1 , C − 1 ; 0 ; 2 , D − 3 ; 2 ; 5 . Tính thể tích tứ diện ABCD.
A. 1 6
B. 1
C. 1 3
D. 1 2
Trong không gian Oxyz. Cho tứ diện đều ABCD có A(0;1;2) và hình chiếu vuông góc của A trên mặt phẳng (BCD) là H (4; -3;-2). Tọa độ tâm I của mặt cầu ngoại tiếp tứ diện ABCD.
A. I(3; -2;-1).
B. I(2;-1;0).
C. I(3; -2;1).
D. I(-3; -2;1).
Trong không gian Oxyz, cho tam giác đều ABC với A (5;3;-1) và B (2;3;-4) điểm C nằm trong mặt phẳng Oxyz có tung độ nhỏ hơn 3.
a) Tìm tọa độ điểm D biết ABCD là tứ diện đều.
b) Tìm tọa độ điểm S biết SA, SB, SC đôi một vuông góc.
Không có mặt phẳng nào là mặt phẳng Oxyz cả nên chắc đề ko đúng. Giả sử nó là Oxy đi
Ý tưởng giải bài toán như sau:
- Viết phương trình mp trung trực (P) của đoạn AB
- Viết pt tham số đường thẳng d là giao của (P) và Oxy
- C thuộc d nên quy tọa độ C về 1 ẩn
- Tính độ dài AB=AC sẽ tìm được tọa độ C
- Viết phương trình mp trung trực (Q) của AC
- Viết pt tham số đường thẳng d1 là giao của (P) và (Q)
- D thuộc d1 => quy tọa độ D theo 1 ẩn, tính độ dài AD=AB => tọa độ D
Câu b thì giải hệ 3 tích vô hướng: SA.SB, SA.SC, SB.SC=0
Chết, ghi lộn đợi mình ăn xong mình tìm lại đề nhé bạn 😁
Trong không gian hệ tọa độ Oxyz, cho tứ diện ABCD với A(2;3;2), B(6;-1;-2), C(-1;-4;3), D(6;-1;-2). Tìm tọa độ điểm M thuộc đường thẳng CD sao cho tam giác ABM có chu vi nhỏ nhất.
A. M(1;1;0)
B. M(0;1;-1)
C. M(1;1;-1)
D. M(-1;1;-1)
Đáp án B.
Ta có:
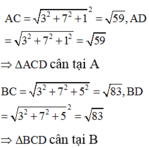
Từ đó gọi M là trung điểm của CD ta có ![]()
Do đó chu vi ∆ A B M là
![]()
(vì AB không thay đổi), tức là khi M là trung điểm cuả CD hay M(0;1;-1)