Đáp án B

+ Xét hàm y = f(x) = cos (x + π)          

TXĐ: D = R

Với mọi x ∈ D, ta có: -x ∈ D và f(-x) = cos (-x + π) = -cos x = cos (x + π) = f(x)

Do đó y = cos (x + π) là hàm số chẵn .

+ Xét hàm y = g(x) = tan²⁰¹⁶x

TXĐ: D = R\{π/2 + kπ, k ∈ Z}

Với mọi x ∈ D, ta có: -x ∈ D và g(-x) = tan²⁰¹⁶(-x) = (-tan x)²⁰¹⁶ = tan²⁰¹⁶x = g(x)  

Do đó: y = tan²⁰¹⁶x là hàm chẵn trên tập xác định của nó.

+Xét hàm y = cot2x

f(-x) = cot(-2x) = - cot 2x = -f(x) nên đây là hàm số lẻ.

+ Xét hàm số  y = 1-sinx

f(-x) = 1- sin(-x) = 1+ sin x

Nên hàm số không chẵn không lẻ

+ Xét hàm  y = f x = cos x + π

TXĐ:  D= R

Với mọi x ∈ D , ta có: − x ∈ D  và

f − x = cos − x + π = − cos x = cos x + π = f x

Do đó y = cos x + π là hàm số chẵn trên R.

+ Xét hàm  y = g x = tan 2016 x

TXĐ:  D = ℝ \ π 2 + k π , k ∈ ℤ

Với mọi x ∈ D , ta có: − x ∈ D  và

g − x = tan 2016 − x = − tan x 2016 = tan 2016 x = g x  

Do đó: y = tan 2016 x là hàm chẵn trên tập xác định của nó

Chọn đáp án B.

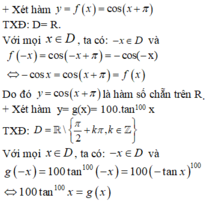
Do đó: y= 100 tan¹⁰⁰x  là hàm chẵn trên tập xác định của nó.

Đáp án B

Đáp án C.

+ Xét hàm y = f(x) = cos 3x

TXĐ: D = R

Với mọi x ∈ D, ta có: -x ∈ D và f(-x) = cos (-3x) = cos 3x = f(x)

Do đó, y = f(x) = cos 3x  là hàm chẵn trên tập xác định của nó.

+ Xét hàm y = g(x) =  sin (x² + 1)

TXĐ: D = R

Với mọi x ∈ D, ta có: -x ∈ D  và g(-x) = sin ((-x)² + 1) = sin (x² + 1) = g(x)

Do đó: y = g(x) = sin (x² + 1) là hàm chẵn trên R.

+ Xét hàm y = h(x) = tan² x

TXĐ: D = R\{π/2 + k2π, k ∈ Z)

Với mọi x ∈ D, ta có: -x ∈ D  và h(-x) = tan² (-x) = tan² x = h(x)

Do đó: y = h(x) = tan² x  là hàm số chẵn trên D

+ Xét hàm y = t(x) = cot x.

TXĐ: D = R\{kπ, k ∈ Z)

Với mọi x ∈ D, ta có: -x ∈ D và t(-x) = cot (-x) = -cot x = -t(x)

Do đó: y = t(x) = cot x là hàm số lẻ trên D.

a) + Hàm số y = cos x có chu kì 2π.

Do đó: cos 2.(x + kπ) = cos (2x + k2π) = cos 2x.

⇒ Hàm số y = cos 2x cũng tuần hoàn với chu kì π.

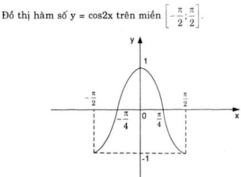
Từ đó suy ra

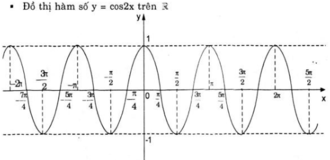
b. y = f(x) = cos 2x

⇒ y’ = f’(x) = (cos 2x)’ = -(2x)’.sin 2x = -2.sin 2x.

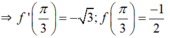
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3 là:

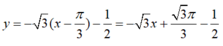
c. Ta có: 1 – cos 2x = 2.sin2x ≥ 0.

Và 1 + cos22x > 0; ∀ x

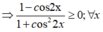
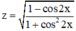⇒  luôn xác định với mọi x ∈ R.

Phương trình hoàn độ giao điểm của hai đồ thì hàm số là \(\sin x = \cos x\)

\( \Leftrightarrow \tan x = 1 \Leftrightarrow x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

Do \(x \in \left[ { - 2\pi ;\frac{{5\pi }}{2}} \right]\; \Leftrightarrow  - 2\pi  \le \frac{\pi }{4} + k\pi  \le \frac{{5\pi }}{2}\;\; \Leftrightarrow \; - \frac{9}{4} \le k \le \frac{9}{4}\;\;\;\)

Mà \(k\; \in \mathbb{Z}\;\; \Leftrightarrow k\; \in \left\{ { - 2;\; - 1;0;1;2} \right\}\)

Vậy ta chọn đáp án A

Đáp án đúng : D