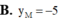
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:
y = − x 3 + 3x + 1
b) Chỉ ra phép biến hình biến (C) thành đồ thị (C’) của hàmsố:
y = ( x + 1 ) 3 − 3x − 4
c) Dựa vào đồ thị (C’), biện luận theo m số nghiệm của phương trình:
( x + 1 ) 3 = 3x + m
d) Viết phương trình tiếp tuyến (d) của đồ thị (C’), biết tiếp tuyến đó vuông góc với đường thẳng
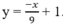
a)
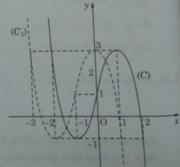
b) Tịnh tiến (C) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị (C1) của hàm số.
y = f(x) = − ( x + 1 ) 3 + 3(x + 1) + 1 hay f(x) = − ( x + 1 ) 3 + 3x + 4 (C1)
Lấy đối xứng (C1) qua trục Ox, ta được đồ thị (C’) của hàm số y = g(x) = ( x + 1 ) 3 − 3x – 4
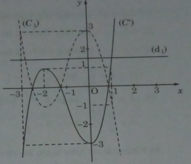
c) Ta có: ( x + 1 ) 3 = 3x + m (1)
⇔ ( x + 1 ) 3 − 3x – 4 = m – 4
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
y = g(x) = ( x + 1 ) 3 − 3x – 4 (C’) và y = m – 4 (d1)
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.
d) Vì (d) vuông góc với đường thẳng:
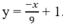
nên ta có hệ số góc bằng 9.
Ta có: g′(x) = 3 ( x + 1 ) 2 – 3
g′(x) = 9 ⇔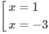 
Có hai tiếp tuyến phải tìm là:
y – 1 = 9(x – 1) ⇔ y = 9x – 8;
y + 3 = 9(x + 3) ⇔ y = 9x + 24.
Phương trình tiếp tuyến với đồ thị (C) của hàm số y = x 3 - 3 x + 1 , biết tiếp tuyến song song với đường thẳng ( d ) : y = 9 x + 17 là
A. y = 9 x + 19 y = 9 x - 21
B. y = 9 x - 19 y = 9 x + 21
C. y = 9 x - 15 y = 9 x + 17
D. y = 9 x - 15
Cho hàm số y = f(x) có đồ thị (C), biết tiếp tuyến của đồ thị (C ) tại điểm có hoành độ x = 0 là đường thẳng y = 3x-3. Giá trị của lim x → 0 3 x f ( 3 x ) - 5 f ( 4 x ) + 4 f ( 7 x ) bằng ?
A. 1 10
B. 3 31
C. 3 25
D. 1 11
Cho hàm số y = f (x) có đồ thị (C), biết tiếp tuyến của đồ thị (C) tại điểm có hoành độ
x = 0 là đường thẳng y = 3x - 3. Giá trị của lim x → 0 3 x f ( 3 x ) − 5 f ( 4 x ) + 4 f ( 7 x )
A. 1 10
B. 3 31
C. 3 25
D. 1 11
Cho hàm số y = 2 x + 1 x + 2 có đồ thị C . Viết phương trình tiếp tuyến của C biết tiếp tuyến song song với đường thẳng ∆ : 3 x - y + 2 = 0 là
A. y = 3 x + 5 , y = 3 x - 8
B. y = 3 x + 14
C. y = 3 x - 8
D. y = 3 x + 14 , y = 3 x + 2
Cho hàm số y = 2 x + 1 x + 2 có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng ∆ : 3 x - y + 2 = 0 là
Cho hàm số \(y=x^3+3x^2-6x+1\) (C)
Viết pt tiếp tuyến của đồ thị (C) biết tiếp tuyến vuông góc với đường thẳng \(y=-\dfrac{1}{18}x+1\) ?
\(y'=3x^2+6x-6\)
Tiếp tuyến vuông góc đường thẳng đã cho nên có hệ số góc thỏa mãn:
\(k.\left(-\dfrac{1}{18}\right)=-1\Rightarrow k=18\)
\(\Rightarrow3x^2+6x-6=18\Rightarrow\left[{}\begin{matrix}x=2\Rightarrow y=9\\x=-4\Rightarrow y=9\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=18\left(x-2\right)+9\\y=18\left(x+4\right)+9\end{matrix}\right.\)
Cho hàm số y = 1 3 x 3 - 2 x 2 + x + 2 có đồ thị (C). Phương trình các tiếp tuyến với đồ thị (C) biết tiếp tuyến song song với đường thẳng d: y = - 2 x + 10 3 là
A. y = - 2 x + 2
B. y = - 2 x - 2
C. y = - 2 x + 10 , y = - 2 x - 2 3
D. y = - 2 x - 10 , y = - 2 x + 2 3
Cho đồ thị (C) của hàm số y = x 3 - 3 x + 2 . Số các tiếp tuyến với đồ thị (C) mà các tiếp tuyến đó vuông góc với đường thẳng d : y = - 1 3 x + 1 là
A. 1
B. 2
C. 3
D. 0
