Tốc độ và li độ của một chất điểm dao động điều hoà có hệ thức v 2 640 + x 2 16 = 1 , trong đó x tính bằng cm, v tính bằng cm/s. Tốc độ trung bình của chất điểm trong mỗi chu kì là
A. 0
B. 32 cm/s
C. 8 cm/s
D. 16 cm/s
Tốc độ và li độ của một chất điểm dao động điều hoà có hệ thức v 2 640 + x 2 16 = 1 , trong đó x tính bằng cm, v tính bằng cm/s. Tốc độ trung bình của chất điểm trong mỗi chu kì là
A. 0
B. 32 cm/s
C. 8 cm/s
D. 16 cm/s
Phương pháp: Áp dụng hệ thức độc lập trong dao động cơ
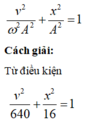
ta có A = 4cm; ω = 40 r a d / s ; T = 0 , 1 π s
Vận tốc trung bình của chất điểm trong mỗi chu kỳ là
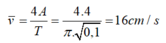
Đáp án D
Một chất điểm dao động điều hoà dọc theo trục Ox, với O trùng với vị trí cân bằng của chất điểm. Đường biểu diễn sự phụ thuộc li độ x chất điểm theo thời gian t ở hình vẽ H1.
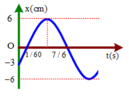
Phương trình vận tốc của chất điểm là
A. v = 12 πcos 2 πt − π 6 cm / s
B. v = 12 πcos 2 πt − 2 π 3 cm / s
C. v = 60 πcos 10 πt − 5 π 6 cm / s
D. v = 60 πcos 10 πt − π 6 cm / s
Một vật dao động điều hoà trên trục Ox với vị trí cân bằng là gốc toạ độ. Gia tốc và li độ liên hệ với nhau bằng biểu thức a = - 4 π 2 x . Số dao động toàn phần vật thực hiện được trong mỗi giây là:
A. 400
B. 40
C. 10
D. 20
Một vật dao động điều hoà trên trục Ox với vị trí cân bằng là gốc toạ độ. Gia tốc và li độ liên hệ với nhau bằng biểu thức a = − 4 π 2 x . Số dao động toàn phần vật thực hiện được trong mỗi giây là:
A. 400
B. 40
C. 10
D. 20
Một chất điểm dao động điều hoà theo phương trình x = 4 3 cos 8 π t ( c m ) , đến vị trí có li độ rong đó t tính theo giây. Thời gian ngắn nhất vật đi từ điểm M có li độ x M = - 6 c m đến vị trí có li độ x N = 6 c m là
A. 1/16 (s)
B. 1/8 (s)
C. 1/12 (s)
D. 1/24 (s)
Đáp án C
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải: Ta có chu kỳ dao động của vật là T = 2 π ω = 2 π 8 π = 1 4 s
Áp dụng vòng tròn lượng giác trong dao động điều hòa ta có
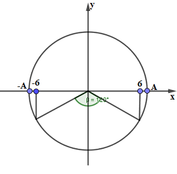
Từ vòng tròn lượng giác ta có để đi từ vị trí x = -6cm đến vị trí x = 6cm vật sẽ quét được trên vòng tròn lượng giác 1 góc 2 π 3
Vì trong một chu kỳ vật quét được 1 góc 2 π do đó ta có:
T ⇔ 2 π = > 2 π 3 = T 3 = 1 4 3 = 1 12 s
Một chất điểm dao động điều hòa với chu kỳ T và biên độ 10cm. Biết trong một chu kỳ , khoảng thời gian để chất điểm có độ lớn vận tốc không vượt quá cm/s là 2T/3. Tính chu kỳ dao động?
Một chất điểm dao động điều hòa với chu kì T . Trong khoảng thời gian ngắn nhất khi đi từ vị trí biên có li độ x=A đến vị trí x = -A/ 2 ,chất điểm có tốc độ trung bình là ?
Tốc độ trung bình = quãng đường / thời gian.
Quãng đường: \(S=A+\dfrac{A}{2}=\dfrac{3A}{2}\)
Biểu diễn dao động bằng véc tơ quay, véc tơ quay được góc là: 90 + 30 = 1200.
Thời gian tương ứng: \(t=\dfrac{120}{360}T=\dfrac{T}{3}\)
Tốc độ trung bình: \(v_{TB}=\dfrac{S}{t}=\dfrac{9A}{2T}=\dfrac{9A.\omega}{2.2\pi}=\dfrac{9v_{max}}{4\pi}\)
Một chất điểm dao động điều hoà theo phương trình ![]() , trong đó t tính theo giây. Thời gian ngắn nhất vật đi từ điểm M có li độ xM = -6cm đến vị trí có li độ xN = 6cm là
, trong đó t tính theo giây. Thời gian ngắn nhất vật đi từ điểm M có li độ xM = -6cm đến vị trí có li độ xN = 6cm là
A. 1/16 (s)
B. 1/8 (s)
C. 1/12 (s)
D. 1/24 (s)
Đáp án C
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải: Ta có chu kỳ dao động của vật là 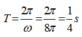
Áp dụng vòng tròn lượng giác trong dao động điều hòa ta có
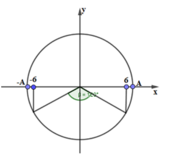
Từ vòng tròn lượng giác ta có để đi từ vị trí x = -6cm đến vị trí x = 6cm vật sẽ quét được trên vòng tròn lượng giác 1 góc ![]()
Vì trong một chu kỳ vật quét được 1 góc 2π do đó ta có: 
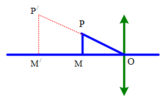
Một thấu kính hội tụ có tiêu cự 15 cm. M là một điểm nằm trên trục chính của thấy kính, P là một chất điểm dao động điều hoà quanh vị trí cân bằng trùng với. Gọi P’ là ảnh của P qua thấu kính. Khi P dao động theo phương vuông góc với trục chính, biên độ 5 cm thì P’ là ảnh ảo dao động với biên độ 10 cm. Nếu P dao động dọc theo trục chính của thấu kính với tần số 5 Hz, biên độ 2,5 cm thì P’ có tốc độ trung bình trong khoảng thời gian 0,2 s bằng:
A. 1,25 m/s
B. 2,25 m/s
C. 1,5 m/s
D. 1 m/s