Có bao nhiêu giá trị nguyên của tham số m ∈ - 2018 ; 2019 để đồ thị hàm số y = x 3 - 3 m x + 3 và đường thẳng y=3x+3 có duy nhất một điểm chung?
A. 1
B. 2019
C. 4038
D. 2018
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018; 2018] để hàm số y = (m – 2)x + 2m đồng biến trên R.
A. 2015
B. 2017
C. Vô số
D. 2016
Hàm số bậc nhất đồng biến suy ra a > 0 hay m > 2
m thuộc đoạn [-2018; 2018] suy ra m thuộc {3; 4; ...; 2018}
Vậy có 2016 giá trị nguyên của m cần tìm.
Chọn D.
Có bao nhiêu giá trị nguyên của tham số m trên [-2018; 2018] để hàm số y = ln ( x 2 - 2 x - m + 1 ) có tập xác định là R
A. 2019
B. 2017
C. 2018
D. 1009
Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 2018 để phương trình m + m + e x = e x có nghiệm thực.
![]()
![]()
![]()
![]()
Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 2018 để phương trình m + m + e x = e x có nghiệm thực.
A. 2016
B. 2017.
C. 2018
D. 2019
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = 1 3 x 3 − 1 2 m x 2 + x + 2018 đồng biến trên R?
A. 5
B. 3
C. 4
D. 2
Đáp án A
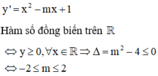
Suy ra có 5 giá trị nguyên của m thỏa mãn đề bài
Cho hàm số y = f x có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số m để hàm số g x = f x + 2018 + m 2 có 5 điểm cực trị?
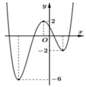
A. 1
B. 2
C. 4
D. 5
Vì hàm f(x) đã cho có 3 điểm cực trị nên f x + 2018 + m 2 cũng luôn có 3 điểm cực trị (do phép tịnh tiến không làm ảnh hưởng đến số cực trị).
Do đó ycbt ⇔ số giao điểm của đồ thị f x + 2018 + m 2 với trục hoành là 2
Để số giao điểm của đồ thị f x + 2018 + m 2 với trục hoành là 2 ta cần
• Tịnh tiến đồ thị f(x) xuống dưới tối thiểu 2 đơn vị ![]()
• Hoặc tịnh tiến đồ thị f(x) lên trên tối thiểu 2 đơn vị nhưng phải nhỏ hơn 6 đơn vị
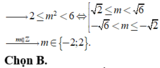
Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây: có bao nhiêu giá trị nguyên của tham số m để hàm số y = f ( x + 2018 ) + m 2 có 5 điểm cực trị
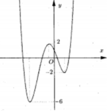
B. 1
C. 2
D. 3
Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2018 để hàm số y = 2 x 3 + 3 ( m - 1 ) x 2 + 6 ( m - 2 ) x + 3 nghịch biến trên khoảng có độ dài lớn hơn 3.
A. 2009
B. 2010
C. 2011
D. 2012
3. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=\dfrac{x+1}{x+3m}\) nghịch biến trên khoảng(6;+\(\infty\) )?
4. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=\dfrac{x+2}{x+3m}\) đồng biến trên khoảng (-\(\infty\);-6)?
3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)
Có bao nhiêu giá trị nguyên của m lớn hơn -2018 để hàm số y = − x 3 − 3 x 2 + 4 m x − 2018 nghịch biến trên ( − ∞ ; 0 ) ?
A. 2017
B. 2018
C. 2019
D. Vô số