Cho lăng trụ đứng A B C D . A ' B ' C ' D ' có đáy là hình thoi cạnh a, góc B A D ^ = 60 ° ; A A ' = a 2 . M là trung điểm của AA’ . Gọi φ của góc giữa hai mặt phẳng ( B ' M D và A B C D . Khi đó c os φ bằng:
A. 3 3
B. 3 4
C. 2 3
D. 5 3
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi, cạnh a; \(\widehat{BAD}=60^0\). Biết \(AB'\perp BD'\). Tính thể tích khối lăng trụ \(\left(V=S_đ.h\right)\)
Đặt \(x=AA'\)
Ta có: \(\overrightarrow{AB'}=\overrightarrow{AA'}+\overrightarrow{AB}\) ; \(\overrightarrow{BD'}=\overrightarrow{BB'}+\overrightarrow{BD}=\overrightarrow{BB'}+\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{AB'}.\overrightarrow{BD'}=\left(\overrightarrow{AA'}+\overrightarrow{AB}\right)\left(\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=AA'^2+\overrightarrow{AA'}\left(-\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{AB}.\overrightarrow{AA'}-AB^2+\overrightarrow{AB}.\overrightarrow{BC}\)
\(=x^2-a^2+AB.BC.cos120^0\)
\(=x^2-a^2-\dfrac{a^2}{2}=x^2-\dfrac{3a^2}{2}=0\)
\(\Rightarrow x=\dfrac{a\sqrt{6}}{2}\)
\(V=\dfrac{a\sqrt{6}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{2}}{4}\)
Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình thoi cạnh bằng a và A B C ⏜ = 120 ° . Góc giữa cạnh bên AA' và mặt đáy bằng 60 ° , điếm A’ cách đều các điểm A, B, D . Tính thể tích khối lăng trụ đã cho theo a.
A. a 3 3 3
B. a 3 3 2
C. a 3 3 12
D. a 3 3 6
Cho lăng trụ đứng A B C D . A ' B ' C ' D ' có đáy ABCD là hình thoi có độ dài cạnh 3cm, góc ∠ A B C = 60 o và chiều cao AA’ của hình lăng trụ bằng 4cm. Tính:
a) Diện tích xung quanh của hình lăng trụ.
b) Thể tích của hình lăng trụ đó.
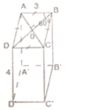
a) Sxq = 2.P.H (p: chu vi đáy; h: chiều cao)
= 3(3 + 3).4 = 48(cm2)
b) Gọi O là giao điểm của AC và BD. Vì tứ giác ABCD là hình thoi nên AC ⊥ BD tại O và có ∠ABC = 60o => ∠ABO = 30o
ΔABO là nửa tam giác đều nên
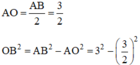
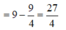
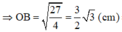
![]()
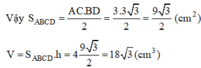
Cho hình lăng trụ đứng ABCD.A'B'C'D’ có đáy là hình thoi cạnh 3 cm, A B C ^ = 60 ° và chiều cao bằng 5 cm.
a) Tính diện tích xung quanh lăng trụ.
b) Tính diện tích toàn phần lăng trụ.
c) Tính thể tích lăng trụ.
Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy là hình vuông cạnh bằng 4cm, đường chéo AB′ của mặt bên (ABB′A′) có độ dài bằng 5cm. Tính thể tích V của khối lăng trụ ABCD.A′B′C′D′.
A. 48 cm 3
B. 24 cm 3
C. 16 cm 3
D. 32 cm 3
Tính diện tích xung quanh , diện tích toàn phần và thể tích của lăng trụ đứng có chiều cao h và cạnh đáy lần lượt là: a)hình vuông cạnh a b)Tam giác đều cạnh a c) lục giác đều cạnh a d) hình thang cân,đáy lớn là 2a,các cạnh còn lại a e) hình thoi có 2 đường chéo là 6a và 8a
Cho hình lăng trụ đứng ABCD. 'D ' có ABCD là hình thoi cạnh a, góc giữa đường thẳng A 'B và mặt phẳng (ABCD) bằng 600 . Tính khoảng cách d giữa hai đường thẳng AC và B ' D '
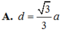
![]()
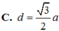
![]()
cho lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh bằng a, góc ABC =60 độ, AA'= 3a. tính thể tích khối lăng trụ đó
Gọi O là tâm hình thoi ABCD.
Do ABCD là hình thoi mà \(\widehat{ABC}=60^o\)
⇒ Tam giác ABC đều.
⇒ \(BO=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
⇒ \(BD=2BO=a\sqrt{3}\)
\(V_{ABCD.A'B'C'D'}=AA'\cdot S_{ABCD}=3a\cdot\dfrac{1}{2}\cdot a\sqrt{3}\cdot a=\dfrac{3a\sqrt{3}}{2}\)
cho hình lăng trụ ABCDA'B'C'D' đáy là hình thoi cạnh A tâm O, góc ABC=120°. góc giữa AA' và đáy là 60°. A' cách đều A,B,D. Tính thể tích ABCDA'B'C'D'
Cho hình lăng trụ A B C D . A ' B ' C ' D ' có đáy ABCD là hình thoi cạnh a, tâm O và A B C = 120 ° . Các cạnh AA', A'B, A' D cùng tạo với đáy một góc 60 ° .Tính theo a thể tích V của khối lăng trụ đã cho.
A. a 3 3
B. a 3 3 6
C. a 3 3 2
D. 3 a 3 2
Đáp án C
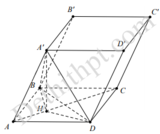
Ta có: A B C ^ = 120 ∘ ⇒ B A D ^ = 60 ∘ suy ra tam giác ABD là tam giác đều cạnh a. Khi đó A’.ABD là chóp đều cạnh đáy bằng a. Như vậy hình chiếu vuông góc của A’ lên mặt đáy trùng với trọng tâm tam giác ABD.
Ta có: A ' H = HA tan 60 ∘ = a 3 3 . 3 = a
⇒ V A ' A B D = 1 3 A ' H . S A B C = a 3 3 12
Do đó V A B C D . A ' B ' C ' D ' = 3 V A ' . A B C D = 6 V A ' A B D = a 3 3 2 .