Chọn D

Hàm số có 2 điểm cực trị  x 1 , x 2

Chia y cho y’ ta được :

Điểm cực trị tương ứng :

Với x 1 + x 2 = 4 x 1 x 2 = m + 2 nên  y 1 y 2 = ( m - 2 ) 2 ( 4 m + 17 )

Hai cực trị cùng dấu  ⇔ y 1 y 2 > 0

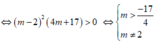
Kết hợp đk :  - 17 4 < m < 2

b: Để hai đường thẳng song song thì

\(\left\{{}\begin{matrix}m^2-2=2\\1-m< >3\end{matrix}\right.\Leftrightarrow m=2\)

1. hàm số nghịch biến khi

\(a< 0\\ \Leftrightarrow m-2< 0\\ \Leftrightarrow m< 2\) 

2. \(y=\left(m-2\right)x+m+3\cap Ox,tại,x=3\)

\(\Rightarrow y=0\)

Có: \(0=\left(m-2\right)3+m+3\\ \Leftrightarrow0=4m-4\\ \Leftrightarrow m=\dfrac{3}{4}\)

3. pt hoành độ giao điểm của 

\(y=-x+2,và,y=2x-1\) là

\(-x+2=2x-1\\ \Leftrightarrow3x=3\Leftrightarrow x=1\Rightarrow y=1\)

A(1,1)

3 đt đồng quy \(\Rightarrow A\in y=\left(m-2\right)x+m+3\\ \Rightarrow1=\left(m-2\right)1+m+3\\ \Leftrightarrow2m=0\\ \Leftrightarrow m=0\)

a: Để hàm số y=(m-2)x+m+3 nghịch biến trên R thì m-2<0

=>m<2

b: Thay x=3 và y=0 vào y=(m-2)x+m+3, ta được:

\(3\left(m-2\right)+m+3=0\)

=>3m-6+m+3=0

=>4m-3=0

=>4m=3

=>\(m=\dfrac{3}{4}\)

c: Tọa độ giao điểm của hai đường thẳng y=-x+2 và y=2x-1 là:

\(\left\{{}\begin{matrix}2x-1=-x+2\\y=-x+2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3x=3\\y=-x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1+1=0\end{matrix}\right.\)

Thay x=1 và y=0 vào y=(m-2)x+m+3, ta được:

\(1\left(m-2\right)+m+3=0\)

=>m-2+m+3=0

=>2m+1=0

=>2m=-1

=>\(m=-\dfrac{1}{2}\)