Tam giác có ABC, C ^ = 150 o , B C = 3 , AC=2. Tính cạnh AB
A. 13
B. 3
C. 10
D. 1
Tam giác ABC có tia phân giác góc B và tia phân giác góc C cắt nhau tại O=150 độ. Tính góc A
Cho tam giác ABC có A ^ = B ^ + C ^ . Hai đường phân giác của góc A và góc C cắt nhau tại O. Khi đó số đo B O C ^ bằng:
A. 85°.
B. 90°.
C. 135°.
D. 150°.
Cho tam giác ABC có ba cạnh a,b,c và có chu vi 2p, diện tích S thỏa \(\frac{\sqrt{3}}{36}\)(a+b+c)^2. Hỏi tam giác ABC là tam giác gì ?
Cho tam giác ABC. Vẽ điểm O cách đều ba đỉnh A, B, C trong mỗi trường hợp sau:
a) Tam giác ABC nhọn;
b) Tam giác ABC vuông tại A;
c) Tam giác ABC có góc A tù.
a) Tam giác ABC nhọn:
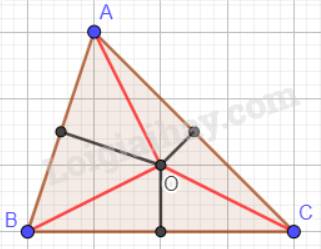
b) Tam giác ABC vuông tại A:
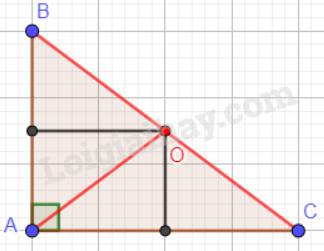
c) Tam giác ABC có góc A tù:
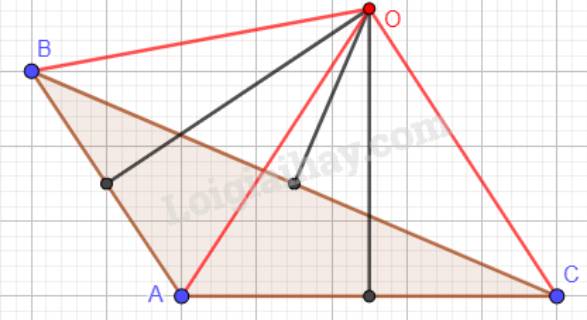
Cho tam giác ABC có B\(=\)80o, C=30o. Tia phân giác của góc A cắt BC ở D. Tính góc ADC và góc ADB
Xét tam giác ABC có
góc A + góc B + góc C = 180^0
góc A + 80^0 + 30^0 = 180^0
góc A + 110^0 = 180^0
góc A = 180^0 - 110^0
góc A = 70^0
Vì tia AD là tia phân giác của góc A nên:
góc A1 = góc A2 = góc A/2 = 70^0/2 = 35^0
Xét tam giác ADB có :
góc A2 + góc B + góc ADB = 180^0
35^0 + 80^0 + góc ADB = 180^0
115^0 + góc ADB = 180^0
góc ADB = 180^0 - 115^0
góc ADB = 65^0
Xét tam giác ADB có :
góc A1 + góc C + góc ADC = 180^0
35^0 + 30^0 + góc ADC = 180^0
65^0 + góc ADC = 180^0
góc ADC = 180^0 - 65^0
góc ADC = 115^0
( Có thể giải nhiều cách nha bạn . Ví dụ như áp dụng góc ngoài của tam giác hay là theo cách của mình sao cũng được ! )
2, Cho Tam giác ABC có góc B > Góc C. Đường phân giác góc ngoài BAx cắt tia CB tại E.
a, CMR: góc AEB = góc \(\frac{B-C}{2}\)
b, Tính số đo B,C của Tam giác ABC với góc A = 60 độ và AEB = 15 độ
3, Cho tam giác ABC và điểm O nằm trong tam giác
a, CMR : góc BOC = góc A + góc ABO + góc ACO
b, Biết góc ABO + góc ACO=90 - \(\frac{A}{2}\)và tia BO: tia p/g của góc B. CMR: CO: tia phân giác của góc C
Cho tam giác ABC co góc BAC=50\(^o\).O là giao diểmcuar 2 tia phân giác cua góc B và C.
a) Tính góc BOC
b)Điểm O có cách đều 3 cạnh của tam giác không?Tại sao
c) Kẻ tia AD.Tính góc BAO
HUHU CÁC BẠN GIÚP MÌNH NHA MAI MÌNH THI RÙI
a) Ta có : góc ABC + góc ACB= 130 độ (tự chứng minh)
=> 2 lần góc OBC + 2 lần góc OCB = 130 độ
=> 2 (góc OBC + góc OCB) = 130 độ
=> góc OBC + góc OCB = 65 độ
Xét tam giác OBC có : góc OBC + góc OCB = 65 độ
=> góc BOC = 180 độ - 65 độ = 115 độ
Cho tam giác ABC có C=\(30^o\) , \(B= 44^o\) và AC = 7. Tính diện tích tam giác ABC và bán kính đường tròn nội tiếp tam giác ABC.
\(\widehat{A}=180^o-30^o-44^o=106^o.\)
Áp dụng định lý sin ta có:
\(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}=\dfrac{AB}{sinC}.\)
\(\Rightarrow\dfrac{BC}{sin106^o}=\dfrac{7}{sin44^o}=\dfrac{AB}{sin30^o}.\)
\(\Rightarrow\left\{{}\begin{matrix}BC=\dfrac{7.sin106^o}{sin44^o}\approx9,7.\\AB=\dfrac{7.sin30^o}{sin44^o}\approx5,0.\end{matrix}\right.\) (đvđd).
\(S_{\Delta ABC}=\dfrac{1}{2}AB.AC.\sin A\approx\dfrac{1}{2}.5,0.7.\sin106^o\approx17,4\) (đvdt).
\(S=pr=\dfrac{AB+AC+BC}{2}.r.\\ \Rightarrow17,4\approx\dfrac{5,0+7+9,7}{2}.r.\)
\(\Rightarrow r\approx1,6\) (đvđd).
Cho tam giác ABC cân tại A ( góc A < 90 độ) có AM là đường phân giác
a) Cm: \(\Delta MAB=\Delta MAC\)
b) Đường cao BE của tam giác ABC cắt AM tại H. Cmr: CH vuông góc với AB
c) Trên cạnh AB lấy điểm O sao cho AO = AE. Cmr: C, H, O thẳng hàng
a) Xét tam giác MAB và MAC có:
AB = AC (tam giác ABC cân tại A)
Góc BAM = CAM (do AM là p/g của góc A)
Cạnh chung AM
=> tam giác MAB = MAC (c - g - c)
b) Tam giác ABC cân tại A có AM là p/g nên đông thời là đường cao
Có BE là đường cao
BE giao với AM tại H
=> H là trực tâm của tam giác ABC => CH vuông góc với AB
c) Xét tam giác AOH và AEH có:
AO = AE
góc OAH = HAE
cạnh chung AH
=> tam giác AOH = AEH (c- g- c)
=> góc AOH = AEH
mà góc AEH = 90 độ
=> góc AOH = 90 độ => AO vuông góc với OH hay AB vuông góc với OH
mà CH vuông góc với AB
=> OH trùng với CH => C; O; H thẳng hàng
a) vì AM là đường phân giác => góc BAM= góc CAM
Xét hai tam giác ABM và ACM có:
AB=AC( do tam giác ABC cân tại A=>AB=AC)
Góc BAM= góc CAM
cạnh AM chung
==>> tam giác ABM= tam giác ACM(c.g.c)
Mình chỉ c/m cho phần a thui,xin lỗi nha
Cho tam giác ABC có AB = 12; \(\widehat B = {60^o}\); \(\widehat C = {45^o}\). Tính diện tích của tam giác ABC.
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {60^o}.\frac{{12}}{{\sin {{45}^o}}} = 6\sqrt 6 \)
Lại có: \(\widehat A = {180^o} - ({60^o} + {45^o}) = {75^o}\)
\( \Rightarrow \)Diện tích tam giác ABC là:
\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.12.6\sqrt 6 .\sin {75^o} \approx 85,2\)
Vậy diện tích tam giác ABC là 85,2.