Đáp án là A
Theo định lí cosin trong tam giác ABC ta có:
![]()
![]()
Đáp án là A
Theo định lí cosin trong tam giác ABC ta có:
![]()
![]()
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại C, có cạnh AB a = , cạnh bên SA vuông góc mặt phẳng đáy và SA a = 3 . Tính thể tích V khối cầu ngoại tiếp hình chóp.
A. V= 2 2 3 3 a .
B. V= 3 4a .
C. V= 32 3 3 πa .
D. V= 4 3 3 πa .
Trong không gian, cho tam giác ABC vuông tại A, AB = a và AC = a 3 . Khi quay tam giác ABC xung quanh AB, ta được một khối nón có độ dài đường sinh là:
A. l = 2a B. l = a 2
C. l = a 3 D. l = a
Cho tam giác ABC vuông tại A, BC=a, AC=b, AB=c, b<c. Khi quay tam giác vuông ABC một vòng quanh cạnh BC, quanh cạnh AC, quanh cạnh AB, ta được các hình có diện tích toàn phần theo thứ tự bằng S a , S b , S c . Khẳng định nào dưới đây đúng?
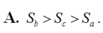
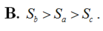
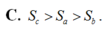
![]()
Cho tam giác ABC vuông tại A. AB=c, AC=b. Quay tam giác ABC xung quanh đường thẳng chứa cạnh AB được một hình nón có thể tích bằng:
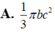
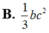
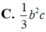
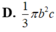
Cho tam giác ABC vuông tại A, AB=c, AC=b. Quay tam giác ABC xung quanh đường thẳng chứa cạnh AB ta được một hình nón có thể tích bằng
![]()
![]()
![]()
![]()
Xho 4 điểm vectow a(2:0:1) b(1:-1:2) c(2:3:1)d(2:-3:2)
Cm tam giác abc có góc a là tù
Tìm chu vi và diện tích tam giác abc
Tìm M thuộc oy sao cho tam giác mbc vuong góc m
Tính thể tích abcd
Hình chóp S.ABC có đáy ABC là tam giác vuông tại C. Có CA = a,CB = b cạnh SA = h vuông góc với đáy. Gọi D là trung điểm của cạnh AB. Khoảng cách giữa hai đường thẳng AC và SD là?
A. a h a 2 + h 2 .
B. b h b 2 + 4 h 2 .
C. a h b 2 + 4 h 2 .
D. a h b 2 + 2 h 2 .
Cho tam giác ABC vuông tại A có BC = 2a và ∠ B = 30 ° . Quay tam giác vuông này quanh trục AB, ta được một hình nón đỉnh B. Gọi S 1 là diện tích toàn phần của hình nón đó và S 2 là diện tích mặt cầu đường kính AB. Khi đó, tỉ số S 1 / S 2 là:
A. 1 B. 1/2
C. 2/3 D. 3/2
Cho hình lăng trụ đứng ABC.A' B' C' có đáy ABC là tam giác vuông tại A, biết AB = a, AC = 2a và A' B = 3a. Tính thể tích của khối lăng trụ ABC.A' B' C'.
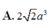
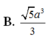
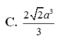
![]()