Đáp án B
Hướng dẫn giải:
Dựng hình bình hành ACDK
![]()
![]()
+Kẻ A P ⊥ D K ⇒ 1 d 2 = 1 S A 2 + 1 A P 2
+ Gọi M = B C ∩ D K
⇒ A C M P l à h i n h c h ữ n h a t
⇒ A P = C M = b 2
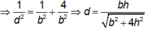
Đáp án B
Hướng dẫn giải:
Dựng hình bình hành ACDK
![]()
![]()
+Kẻ A P ⊥ D K ⇒ 1 d 2 = 1 S A 2 + 1 A P 2
+ Gọi M = B C ∩ D K
⇒ A C M P l à h i n h c h ữ n h a t
⇒ A P = C M = b 2
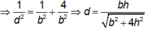
Cho hình chóp tam giác S.ABC có SA vuông góc với mặt đáy, tam giác ABC cân tại A. Trên cạnh AB lấy điểm D sao cho AB = 3AD. Gọi H là hình chiếu của B lên CD, M là trung điểm CH. Tính theo a thể tích khối chóp S.ABM biết SA = AM = a và BM = 2/3 a
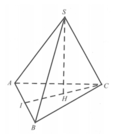
Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a, gọi I là trung điểm của AB, hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của CI, góc giữa SA và mặt đáy bằng 45 ∘ (tham khảo hình vẽ bên dưới). Khoảng cách giữa 2 đường thẳng SA và CI bằng:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC=2a, SA vuông góc với mặt phẳng đáy và SA=a 3 . Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng:
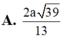
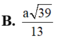
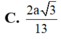
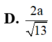
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA=3HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tính khoảng cách giữa hai đường thẳng SA và BC theo a
A. a 61 4
B. 4 a 17 3
C. a 35 51
D. 4 a 351 3 61
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, cạnh AB = 2, A B C ^ = 60°. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Góc giữa SA và mặt phẳng đáy bằng 45°. Tính thể tích khối chóp S.ABC.
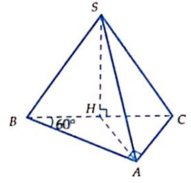
A. 4 3
B. 2 3
C. 2
D. 4 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = a , A D = a 2 . Gọi H là trung điểm của cạnh AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng (SAC) và (ABCD) là 60 ° . Tính khoảng cách giữa hai đường thẳng CH và SD
A. 2 a 5 5
B. 2 a 10 5
C. a 5 5
D. 2 a 2 5
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SA vuông góc với mặt phẳng (ABC). Biết rằng A B = a , A C = a 3 và S B A ^ = 60 ° . Gọi H là hình chiếu vuông góc của A trên cạnh SC. Tính tỷ số thể tích của hai khối SABH và HABC
A. 3 4
B. 1 12
C. 3 2
D. 1
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=3a, BC=4a. Cạnh bên SA vuông góc với đáy. Góc tạo bởi giữa SC với đáy bằng 60 0 . Gọi M là trung điểm AC, tính khoảng cách giữa hai đường thẳng AB và SM
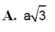
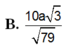
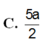
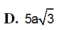
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = 2a, cạnh SA vuông góc với đáy và SA = 2a. Khoảng cách giữa hai đường thẳng AB và SC là
A . a 3
B . 2 a
C . a 2
D . a 5