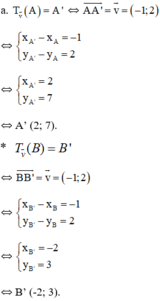
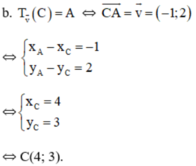
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)

=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d

=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.

Nên đường thẳng d’ có dạng : x- 2y + m= 0

Lại có B(-1; 1) d nên B’(-2;3) d’

Thay tọa độ điểm B’ vào phương trình d’ ta được:

-2 -2.3 +m =0 ⇔ m= 8

Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0

Đáp án D

(d) biến thành chính nó khi vecto tịnh tiến cùng phương với (d). Mà (d) có một VTCP là  1 ; 2

Gọi M′(x′;y′) ∈ d′ là ảnh của M(x,y) ∈ d qua phép tịnh tiến theo vecto  v → ( 2 ; 3 )

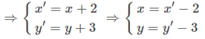
Do M(x,y) ∈ d nên

3x − 5y + 3 = 0

⇒ 3(x′−2) − 5(y′−3) + 3 = 0

⇔ 3x′ − 5y′ + 12 = 0 (d′)

Vậy M′(x′;y′) ∈ d′: 3x′ − 5y′ + 12 = 0

Chọn D

Thực hiện phép đối xứng tâm O biến d thành d’, sau đó thực hiện phép tịnh tiến theo  u →   biến d’ thành đường  thẳng d”.

* Qua phép đối xứng tâm O: biến điểm M(x; y) thuộc d thành điểm M’(x’; y’) thuộc d’.

Ta có: x ' = − x y ' = − y   ⇔ x = − x ' y = − y '    Vì M thuộc d nên:  x+ y – 2 = 0 . Suy ra:

 -x’ + (- y’) – 2 = 0 hay x’+ y’ + 2= 0  

Phương trình đường thẳng d’ : x + y + 2 = 0

* Qua phép đối xứng tịnh tiến theo  ( 3; 2) biến điểm A(x; y) thuộc đường thẳng d’ thành điểm A’ (x’; y’) thuộc đường thẳng d”. Ta có:

  A ​​ A ' → =   u → ⇔ x ' − x = 3 y ' − y = 2   ⇔ x = x ' − ​ 3 y = y ' −    2  

  Vì điểm A thuộc đường thẳng d’ nên: x+ y + 2 =0

Suy ra: (x’ - 3) +  (y’ - 2) + 2 = 0 hay x’ + y’ - 3 = 0

 Phương trình đường thẳng d”  là x + y – 3 = 0

Đáp án D

Dùng các biểu thức tọa độ của các phép biến hình.

Đáp án D

Đáp án B

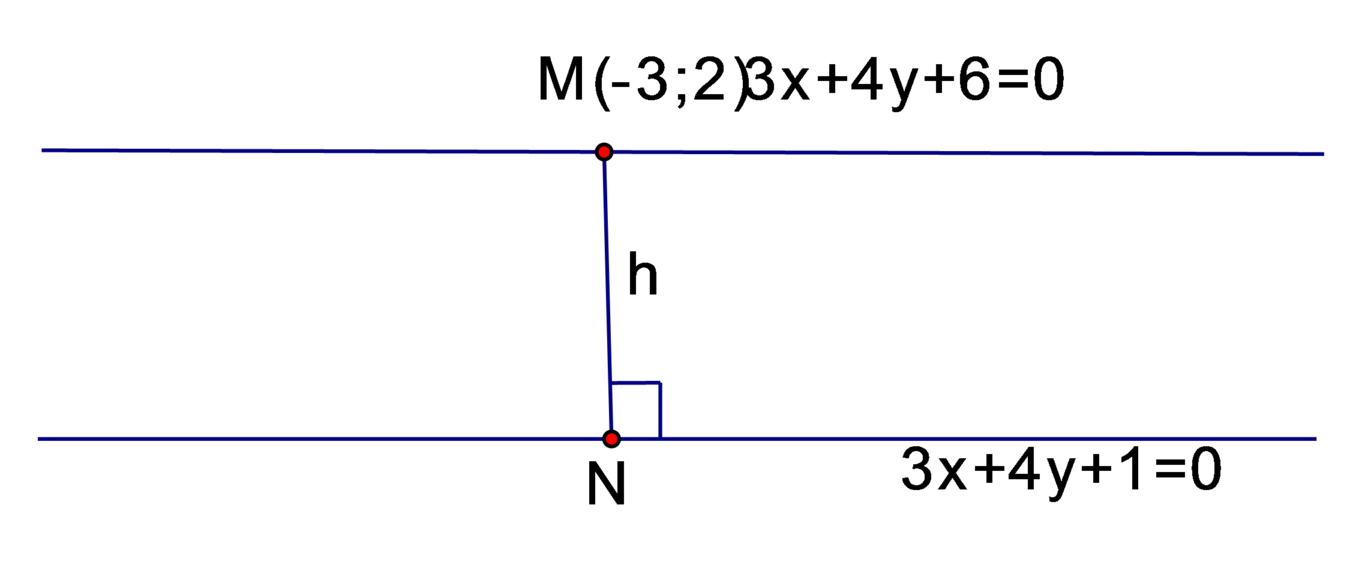
Độ dài véc tơ v →  bé nhất đúng bằng khoảng cách h giữa d và d' . h chính là khoảng cách từ M ∈ d  tới N ∈ d ' sao cho M N → ⊥ u → 4 ; − 3 trong đó u → là VTCP của cả d và d' .Và khi đó:  v → = M N →

Chọn M − 3 ; 2 ∈ d . Ta cần tìm N t ; − 6 − 3 t 4 ∈ d ' sao cho:

M N → t + 3 ; − 14 − 3 t 4 ⊥ u → 4 ; − 3

⇔ 4 t + 12 + 42 + 9 t 4 = 0 ⇔ t = − 18 5

⇒ M N → = − 3 5 ; − 4 5