Tính nguyên hàm I = ∫ d x x x 2 + 4 bằng cách đặt t = x 2 + 4 , mệnh đề nào dưới đây đúng?
A. I = ∫ d t t 2 - 4
B. I = 1 2 ∫ d t t 2 - 4
C. I = ∫ d t t - 4
D. I = ∫ t d t t 2 - 4
Biết F(x) là nguyên hàm của f(x) trên R thỏa mãn ∫ 1 e F ( x ) d ( ln x ) = 3 và F(e)=5 Tính I = ∫ 1 e ln x . f ( x ) d x
A. I = 3
B. I = –3
C. I = 2
D. I = –2
Cho hàm số f(x) có nguyên hàm là F(x) trên đoạn [1;2], biết F(2) = 1 và ∫ 1 2 F ( x ) d x = 5 . Tính I= ∫ 1 2 ( x - 1 ) f ( x ) d x
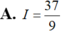
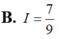
![]()
![]()
Cho hàm số f(x) có nguyên hàm là F(x) trên đoạn [1;2], biết F(2)=1 và ∫ 1 2 F ( x ) d x = 5 . Tính I = ∫ 1 2 ( x - 1 ) f ( x ) d x
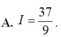
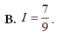
![]()
![]()
Cho F ( x ) = 1 2 x 2 là một nguyên hàm của hàm số f ( x ) x . Tính I = ∫ 1 e f ' ( x ) ln x d x :
A. I = 3 − e 2 2 e 2
B. I = e 2 − 3 2 e 2
C. I = 2 − e 2 e 2
D. I = e 2 − 2 e 2
Tính nguyên hàm I = ∫ x - 2 sin 3 x d x = - x - 2 cos 3 x a + b sin 3 x + C . Tính M = a + 27 b . Chọn đáp án đúng:
A. 6
B. 14
C. 34
D. 22
Tính nguyên hàm \(I=\int\frac{x^4+x^2+1}{x\left(x-2\right)\left(x+2\right)}\)
Đây là nguyên hàm của phân thức hữu tỉ không thực sự. Ta cần tách phần nguyên của phân thức
\(\frac{x^4+x^2+1}{x\left(x-2\right)\left(x+2\right)}=x+\frac{5x^2+1}{x\left(x-2\right)\left(x+2\right)}\)
Triển khai phân thức hữu tỉ thực sự thành tổng các phân thức đơn giản
\(\frac{5x^2+1}{x\left(x-2\right)\left(x+2\right)}=\frac{A_1}{x}+\frac{A_2}{x-2}+\frac{A_3}{x+2}\)
Ta tính được \(A_1=-\frac{1}{4},A_2=\frac{21}{8},A_3=\frac{21}{8}\)
Do đó :
\(I=\frac{1}{2}x^2+\int\frac{-\frac{1}{4}}{x}dx+\int\frac{\frac{21}{8}}{x-2}dx+\int\frac{\frac{11}{8}}{x+2}dx\)
\(=\frac{1}{2}x^2-\frac{1}{4}\ln\left|x\right|+\frac{21}{8}\ln\left|x-2\right|+\frac{21}{8}\ln\left|x+2\right|+C\)
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = sin 3 x . cos x . Tính I = F π 2 - F ( 0 )
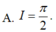
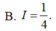
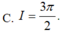
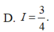
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = sin 3 x cos x . Tính I = F ( π 2 ) - F ( 0 )
A. I = π 2
B. I = 1 4
C. I = 3 π 2
D. I = 3 4
Cho F(x) là một nguyên hàm của hàm số f(x) trên đoạn [1;3], F(1)=3,F(3)=5 và ∫ 1 3 ( x 4 - 8 x ) f ( x ) dx = 12 . Tính I = ∫ 1 3 ( x 3 - 2 ) F ( x ) dx .
A. I= 147 2
B. I= 147 3
C. I= - 147 2
D. I= 147.
Biết F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a;b] và 2F(a)-1=2F(b). Tính I = ∫ a b f ( x ) d x
A. I=-1
B. I=1
C. I = - 1 2
D. I = 1 2