Các câu hỏi tương tự
Biết F(x) là một số nguyên hàm của hàm số f(x) trên đoạn [-1;0],
F
-
1
-
1
;
F
0
0
và
∫
-
1...
Đọc tiếp
Biết F(x) là một số nguyên hàm của hàm số f(x) trên đoạn [-1;0], F - 1 = - 1 ; F 0 = 0 và ∫ - 1 0 2 3 x F ( x ) dx = - 1 . Tính I= ∫ - 1 0 2 3 x f ( x ) dx .
A. 1 8 - 3 ln 2
B. 1 8 + ln 2
C. 1 8 + 3 ln 2
D. - 1 8 + 3 ln 2
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(a,b,cÎR, a≠0) có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số
y
f
’
(
x
)
cho bởi hình vẽ. Giá trị
f
(
3
)
-
2...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a,b,cÎR, a≠0) có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số y = f ’ ( x ) cho bởi hình vẽ. Giá trị f ( 3 ) - 2 f ( 1 ) là
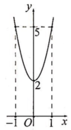
A. 30
B. 24
C. 26
D. 27
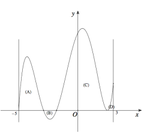
Cho hàm số f(x) xác định và liên tục trên đoạn [-5;3] có đồ thị như hình vẽ bên. Biết diện tích các hình phẳng (A),(B),(C),(D) giới hạn bởi đồ thị hàm số f (x) và trục hoành lượt bằng 6;3;12;2. Tích phân
∫
-
3
1
(
2
f
(
2
x
+
1
)
+
1
)
d
x
bằng A. 27. B. 25. C. 17. D. 21.
Đọc tiếp
Cho hàm số f(x) xác định và liên tục trên đoạn [-5;3] có đồ thị như hình vẽ bên. Biết diện tích các hình phẳng (A),(B),(C),(D) giới hạn bởi đồ thị hàm số f (x) và trục hoành lượt bằng 6;3;12;2. Tích phân ∫ - 3 1 ( 2 f ( 2 x + 1 ) + 1 ) d x bằng
A. 27.
B. 25.
C. 17.
D. 21.
Biết F(x) là nguyên hàm của hàm số
f
x
3
x
4
-
2
x
3
-
1
x
2
và F(1) + 2F(2) 40. Tính F(-1). A. 8 B. 7 C. -8 D. 0
Đọc tiếp
Biết F(x) là nguyên hàm của hàm số f x = 3 x 4 - 2 x 3 - 1 x 2 và F(1) + 2F(2) = 40. Tính F(-1).
A. 8
B. 7
C. -8
D. 0
Cho F(x) là một nguyên hàm của hàm số f(x) trên đoạn [1;3], F(1)3,F(3)5 và
∫
1
3
(
x
4
-
8
x
)
f
(
x
)
dx
12
.
Tính
I
∫
1
3
(
x
3
-
2
)
F
(
x...
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f(x) trên đoạn [1;3], F(1)=3,F(3)=5 và ∫ 1 3 ( x 4 - 8 x ) f ( x ) dx = 12 . Tính I = ∫ 1 3 ( x 3 - 2 ) F ( x ) dx .
A. I= 147 2
B. I= 147 3
C. I= - 147 2
D. I= 147.
Cho hàm số f(x) xác định trên
(
-
∞
;
-
1
)
∪
(
0
;
+
∞
)
thỏa mãn
f
(
x
)
1
x
2
+
x
,
f
(
1
)
ln
1...
Đọc tiếp
Cho hàm số f(x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) thỏa mãn f ' ( x ) = 1 x 2 + x , f ( 1 ) = ln 1 2 . Cho ∫ 1 2 ( x 2 + 1 ) 2 f ( x ) d x =a ln3+b ln2+c, với a,b,c là các số hữu tỷ. Giá trị biểu thức a+b+c bằng
A. 27 20
B. 23 20
C. - 27 20
D. - 23 20
Cho hàm số f(x) thỏa mãn
∫
0
1
x
+
10
f
x
d
x
1
và 2f(12) – f(0) Tính
I
∫
0
1
f
x
d
x
A. I 1. B. I 8 C. I -12 D. I -8
Đọc tiếp
Cho hàm số f(x) thỏa mãn ∫ 0 1 x + 10 f ' x d x = 1 và 2f(12) – f(0) = Tính I = ∫ 0 1 f x d x
A. I = 1.
B. I = 8
C. I = -12
D. I = -8
Biết hàm số
F
(
x
)
a
x
3
+
(
a
+
b
)
x
2
+
(
2
a
-
b
+
c
)
x
+
1
là một nguyên hàm của hàm số
f
(
x
)
3
x
2
+
6...
Đọc tiếp
Biết hàm số F ( x ) = a x 3 + ( a + b ) x 2 + ( 2 a - b + c ) x + 1 là một nguyên hàm của hàm số f ( x ) = 3 x 2 + 6 x + 2 . Tổng a+b+c là:
A. 5
B. 4
C. 3
D. 2
Cho f(x) và g(x) là hai hàm số liên tục trên đoạn [1;3], thỏa mãn:
∫
1
3
[
f
(
x
)
+
3
g
(
x
)
]
d
x
10
và
∫
1
3
[
2
f
(
x
)
-
g
(
x
)
]
d
x...
Đọc tiếp
Cho f(x) và g(x) là hai hàm số liên tục trên đoạn [1;3], thỏa mãn: ∫ 1 3 [ f ( x ) + 3 g ( x ) ] d x = 10 và ∫ 1 3 [ 2 f ( x ) - g ( x ) ] d x = 6 . Tính I = ∫ 1 3 [ f ( x ) + g ( x ) ] d x
A. I=8
B. I=9
C. I=6
D. I=7