Cho hai đường thẳng d : x + y − 1 = 0 và d ' : x + y − 5 = 0 . Phép tịnh tiến theo vecto u → biến đường thẳng d thành d’. Khi đó, độ dài bé nhất của là bao nhiêu?
A. 5
B. 2
C. 2 2
D. 4 2
Cho hai đường thẳng d: y = x + y - 1 = 0 và d': x + y -5 = 0 Phép tịnh tiến theo vecto u → biến đường thẳng d thành d' Khi đó, độ dài bé nhất của u → là bao nhiêu?
A. 2 2
B. 5
C. 2
D. 4 2
Cho hai đường thẳng d: x + y - 1 = 0 và d’: x + y - 5 = 0. Phép tịnh tiến theo vecto u → biến đường thẳng d thành d’. khi đó, độ dài bé nhất của vecto u → là bao nhiêu?
A. 5
B. 4√2
C. 2√2
D. √2
Độ dài bé nhất của vecto u → bằng khoảng cách từ một điểm bất kì trên d tới d’ bằng:
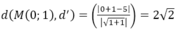
Đáp án C
Cho hai đường thẳng d1 : x+ y -1= 0 và d2 : x- 3y + 3= 0. Phương trình đường thẳng d đối xứng với d1 qua đường thẳng d2 là:
A.x-7y +1 =0
B.x+7y +1= 0
C. 7x+y+1= 0
D. 7x-y+1= 0
Đáp án D
+Giao điểm của d1 và d2 là nghiệm của hệ
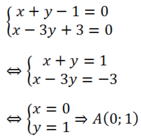
+Lấy M(1 ; 0) thuộc d1. Tìm M’ đối xứng M qua d2
+Viết phương trình đường thẳng ∆ đi qua M và vuông góc với d2 là
3(x-1) + 1( y=0) =0 hay 3x+ y-3= 0
Gọi H là giao điểm của ∆ và đường thẳng d2. Tọa độ H là nghiệm của hệ
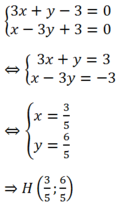
Ta có H là trung điểm của MM’. Từ đó suy ra tọa độ:
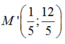
Viết phương trình đường thẳng d đi qua 2 điểm A và M’ : đi qua A(0 ;1) , vectơ chỉ phương 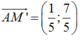
=> vectơ pháp tuyến 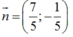
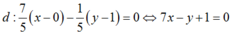
Cho đường thẳng (d): -x+y-2=0 và ∆ 2mx + (m+1)y-3=0. Giá trị của m để hai đường thẳng vuông góc là
A. -1/3
B. – 1
C. 1/3
D. 1
Cho hai đường thẳng d : x + y - 1 = 0 và d ' : x + y - 5 = 0 . Phép tịnh tiến theo vecto u → biến đường thẳng d thành d'. Khi đó, độ dài bé nhất của u → là bao nhiêu?
A. 2 2
B. 5
C. 2
D. 4 2
Đáp án A
Độ dài bé nhất của u → bằng khoảng cách từ một điểm bất kì trên d tới d' bằng
![]()
Cho hai đường thẳng d: 2x- y + 3= 0 và ∆: x+ 3y – 2= 0. Phương trình đường thẳng d’ đối xứng với d qua là:
A. 11x + 13y -2= 0
B.11x -2y = -13
C.13x-11y+3= 0
D.11x-13y+2= 0
Đáp án B
+Giao điểm của d và là nghiệm của hệ
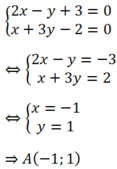
+Lấy M(0; 3) thuộc d. Tìm M’ đối xứng M qua
Viết phương trình đường thẳng đi qua M(0;3) và vuông góc với :
3( x-0) -1( y-3) =0 hay 3x –y+3= 0
+Gọi H là giao điểm của và đường thẳng . Tọa độ H là nghiệm của hệ
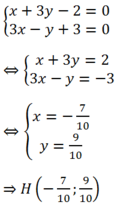
+Ta có H là trung điểm của MM’. Từ đó suy ra tọa độ 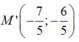
Viết phương trình đường thẳng d’đi qua 2 điểm A và M’: điểm đi qua A( -1 ;1) , vectơ chỉ phương 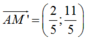
=> vectơ pháp tuyến 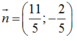
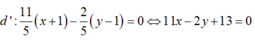
Cho đường thẳng
d : x = 1 y = 1 + t z = - 1 + t
và hai mặt phẳng: (P): x - y + z + 1 = 0 và (Q): 2x + y - z - 4 = 0
Khẳng định nào sau đây là đúng?
A. d // (P) B. d // (Q)
C. d = (P) ∩ (Q) D. d ⊥ (P).
Chọn C.
Đường thẳng d có điểm chung M(1; 1; -1) với cả hai mặt phẳng (P), (Q) và d có vectơ chỉ phương (0; 1; 1) vuông góc với cả hai vectơ pháp tuyến của (P), (Q), do đó d nằm trên cả hai mặt phẳng (P), (Q). Suy ra d = (P) ∩ (Q).
Cho hai đường thẳng d và d'. Tìm m để hai đường thẳng: cắt nhau, song song, đồng quy
a) d: 2mx+(m-1).y-2=0, d': (m+2).x+(2m+1).y-(m+2)=0
b) d: (m-2).x+(m-6).y+m-1=0, d': (m-4).x+(2m-3).y+m-5=0
Cho hai đường thẳng (d): x+2y-1=0 và d’: x-3y+2=0.Số đo góc giữa hai đường thẳng là:
A,600
B,900
C,69034''
D,450
cos(d,d')=\(\dfrac{\left|1.1+2.\left(-3\right)\right|}{\sqrt{1^2+2^2}.\sqrt{1^2+\left(-3\right)^2}}\)= \(\dfrac{\sqrt{2}}{2}\)=450