Cho hình hộp A B C D . A ' B ' C ' D ' có O là giao điểm của AC và BD. Khi đó tỉ số thể tích của khối chóp O . A ' B ' C ' D ' và khối hộp A B C D . A ' B ' C ' D ' bằng.
A. 1 3 .
B. 1 2 .
C. 1 4 .
D. 1 6 .
Cho hình hộp A B C D . A ' B ' C ' D ' có O là giao điểm của AC và BD. Khi đó tỉ số thể tích của khối chóp O . A ' B ' C ' D ' và khối hộp A B C D . A ' B ' C ' D ' bằng.
A. 1 3 .
B. 1 2 .
C. 1 4 .
D. 1 6 .
Đáp án A
Ta có: V A B C D . A ' B ' C ' D ' = B . h , V O . A ' B ' C ' D ' = 1 3 d O ; A ' B ' C ' D ' . B = 1 3 h . B
Cho hình hộp ABCD. A’B’C’D’ gọi O là giao điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’ điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’
A. 1 4
B. 1 3
C. 1 6
D. 1 12
Cho hình hộp chữ nhật đứng A B C D . A ' B ' C ' D ' có A B = a , A D = a , A A ' = 3 a Gọi O ' là tâm hình chữ nhật A ' B ' C ' D ' Thể tích của khối chóp O ' . A B C D là?
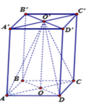
A. 4 a 3
B. 2 a 3
C. a 3
D. 6 a 3
Đáp án B
Gọi O là tâm của hình chữ nhật ABCD thì O O ' = 3 a
V O ' A B C D = 1 3 O O ' . A B . A D = 2 a 3
Cho hình hộp chữ nhật đứng ABCD.A'B'C'D' có AB=a, AD=2a, AA'=3a. Gọi O' là tâm hình chữ nhật A'B'C'D'. Thể tích của khối chóp O'.ABCD là?
A. 4 a 3
B. 2 a 3
C. a 3
D. 6 a 3
Cho khối hộp ABCD. A'B'C'D' có đáy là hình chữ nhật với AB = 3 ; AD = 7 . Hai mặt bên (ABB'A') và (ADD'A') cùng tạo với đáy góc 450, cạnh bên của hình hộp bằng 1 (hình vẽ). Thể tích khối hộp là:
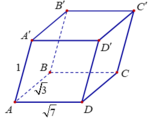
A. 7
B. 3 3
C. 5
D. 7 7
Chọn A
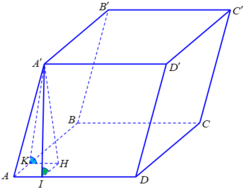
Gọi H là hình chiếu vuông góc của A' lên mặt phẳng (ABCD);

Theo giả thiết, ta có ![]()
=> ΔHKA' = ΔHIA' => HI = HK
=> tứ giác AIHK là hình vuông cạnh a, (a>0) => AH = a√2
Tam giác A'HK vuông cân tại H có HK=HA'=a
Tam giác AHA' vuông tại H có AA'²=AH²+A'H²
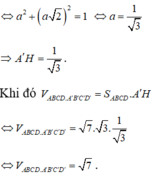
Cho hình hộp chữ nhật ABCD. A’B’C’D’ có thể tích bằng 1 và G là trọng tâm tam giác BCD’ Thể tích V của khối chóp G. ABC’ là
A. V = 1 3
B. V = 1 6
C. V = 1 12
D. V = 1 18
Cho hình lập phương ABCD.A'B'C'D' có O và O' lần lượt là tâm của hình vuông ABCD và A'B'C'D'. Gọi V 1 là thể tích khối nón tròn xoay có đỉnh là trung điểm của OO' và đáy là đường tròn ngoại tiếp hình vuông A'B'C'D', V 2 là thể tích khối trụ tròn xoay có hai đáy là hai đường tròn nội tiếp hình vuông ABCD và A'B'C'D'. Tỉ số thể tích V 1 V 2 là
A. 1 2
B. 3 4
C. 1 4
D. 1 3
Cho hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình vuông cạnh a và cạnh bên bằng 2a. Thể tích khối nón có đỉnh là tâm O của hình vuông A'B'C'D' và đáy là hình tròn ngoại tiếp hình vuông ABCD là:
A. πa 3 3
B. πa 3
C. 2 πa 3 3
D. 2 πa 3 2 3
Đáp án A
Từ giả thiết ta có: h = AA' = 2a;
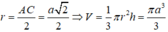
Cho hình lập phương A B C D . A ' B ' C ' D ' . Gọi O, O’ lần lượt là tâm của hai hình vuông ABCD và A ' B ' C ' D ' . Gọi V 1 là thể tích của khối trụ xoay có đáy là 2 đường tròn ngoại tiếp hình vuông ABCD và A ' B ' C ' D ' , V 2 là thể tích khối nón tròn xoay đỉnh O và có đáy là đường tròn nội tiếp hình vuông A ' B ' C ' D ' . Tỷ số thể tích V 1 V 2 là
A. 4
B. 8
C. 6
D. 2
Đáp án C
Gọi cạnh của hình lập phương bằng a
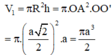
(R là bán kính đường tròn ngoại tiếp hình vuông ABCD)
Thể tích
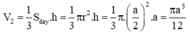
(r là bán kính đường tròn nội tiếp hình vuông ABCD)
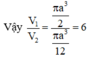
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi O là tâm của mặt đáy ABCD.
a) Chứng minh O.A'B'C'D' là hình chóp tứ giác đều.
b) Gọi thể tích hình chóp đều O.A'B’C'D' là V' và thể tích hình lập phương là V. Tính tỉ số V'/V
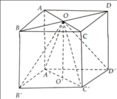
a) Bốn tam giác OAA', OBB', OCC', ODD' là các tam giác vuông bằng nhau nên suy ra OA' = OB' = OC' = OD'.
Hình chóp O.A'B'C'D' là hình chóp đều vì có các mặt bên là tam giác cân và đáy là đa giác đều.
b) Thể tích của của hình chóp O.A'B'C'D' là:
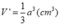
Thể tích hình lập phương:
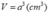
Vậy V ' V = 1 3