Đáp án B
Gọi O là tâm của hình chữ nhật ABCD thì O O ' = 3 a
V O ' A B C D = 1 3 O O ' . A B . A D = 2 a 3
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’
Cho hình hộp chữ nhật
A
B
C
D
.
A
,
B
,
C
,
D
,
có tâm I. Gọi
V
,
V
1
lần lượt là thể tích của khối hộp
A
B
C
D
.
A
,
B
,
C
,
D
,
và khối...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A , B , C , D , có tâm I. Gọi V , V 1 lần lượt là thể tích của khối hộp A B C D . A , B , C , D , và khối chóp I . A B C D Tính tỉ số k = V 1 V .
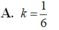
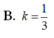
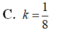
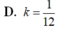
Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật. Tâm của mặt cầu (S) là:
A. Tâm của hình hộp chữ nhật
B. Tâm của một mặt bên của hình hộp chữ nhật
C. Trung điểm của một cạnh của hình hộp chữ nhật
D. Một đỉnh bất kì của hình hộp chữ nhật
Cho khối chóp S.ABCDS.ABCD có đáy là hình chữ nhật, AB=2a,AD=2\sqrt{3}a,SAAB=2a,AD=23a,SA vuông góc với đáy và mặt phẳng (SBC)(SBC) tạo với đáy một góc 60^o60o. Thể tích khối chóp S.ABCDS.ABCD bằng
Cho hình hộp chữ nhật ABCD.ABCD có ABa, ADb,
A
A
c
. Tính thể tích V của khối chóp A.ABCD.
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AD=b, A A ' = c . Tính thể tích V của khối chóp A.A'B'C'D'.
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:A.
π
(
a
2
+
b
2
+
c
2
) B. 2
π
(
a...
Đọc tiếp
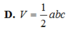
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:
A. π ( a 2 + b 2 + c 2 ) B. 2 π ( a 2 + b 2 + c 2 )
C. 4 π ( a 2 + b 2 + c 2 ) D. π /2.( a 2 + b 2 + c 2 )
Cho hình hộp ABCD.ABCD có đáy là hình chữ nhật, hình chiếu của A lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB a, AD 2a và thể tích hình hộp đã cho bằng 2
a
3
. Khoảng cách từ B đến mặt phẳng (ADCB) bằng:A.
2
a
6
B.
2...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, hình chiếu của A' lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB = a, AD = 2a và thể tích hình hộp đã cho bằng 2 a 3 . Khoảng cách từ B đến mặt phẳng (A'DCB') bằng:
A. 2 a 6 B. 2 a 3
C. 3 a 3 D. a 2
. Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật, AB = 3a, AD = 4a, AA' = 5a. Tính tỷ số thể tích của khối tứ diện ABDA' và khối %3D đa diện BCDD'C'B'A'
Một hình hộp chữ nhật có ba kích thước là
a
,
b
,
c
. Thể tích
V
của khối hộp chữ nhật đó bằng A.
a
+
c
b
B.
a
b
c
C.
a
+
b
c
D.
1
3
a...
Đọc tiếp
Một hình hộp chữ nhật có ba kích thước là a , b , c . Thể tích V của khối hộp chữ nhật đó bằng
A. a + c b
B. a b c
C. a + b c
D. 1 3 a b c