Các câu hỏi tương tự
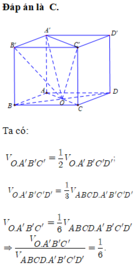
Cho hình hộp ABCD. A’B’C’D’ Tính tỉ số thể tích của khối tứ diện A’C’BD và khối hộp đã cho
A. 1 3
B. 1 6
C. 1 2
D. 1 4
Cho hình hộp chữ nhật ABCD. A’B’C’D’ có thể tích bằng 1 và G là trọng tâm tam giác BCD’ Thể tích V của khối chóp G. ABC’ là A.
V
1
3
B.
V
1
6
C.
V
1
12
D.
V
...
Đọc tiếp
Cho hình hộp chữ nhật ABCD. A’B’C’D’ có thể tích bằng 1 và G là trọng tâm tam giác BCD’ Thể tích V của khối chóp G. ABC’ là
A. V = 1 3
B. V = 1 6
C. V = 1 12
D. V = 1 18
Cho khối chóp S.ABCD có đáy ABCD là hình thoi. Gọi O là giao điểm của AC và BD. Tỉ số thể tích giữa khối chópS.ABCD và S.AOB là: A.
1
2
B.
1
4
C. 2 D. 2
Đọc tiếp
Cho khối chóp S.ABCD có đáy ABCD là hình thoi. Gọi O là giao điểm của AC và BD. Tỉ số thể tích giữa khối chópS.ABCD và S.AOB là:
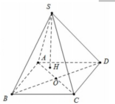
A. 1 2
B. 1 4
C. 2
D. 2
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC và BD. Gọi M, N lần lượt là trung điểm của SB, SC. Tính tỉ số thể tích giữa hai khối chóp O.BCNM và S.ABCD.
Cho hình hộp chữ nhật ABCD. A’B’C’D’ có diện tích các mặt ABCD, BCC’B’, CDD’C’ lần lượt là
2
a
2
,
3
a
2
,
6
a
2
. Tính thể tích khối hộp chữ nhật ABCD. A’B’C’D’ A.
36
a
3
B.
6
a
3
C. ...
Đọc tiếp
Cho hình hộp chữ nhật ABCD. A’B’C’D’ có diện tích các mặt ABCD, BCC’B’, CDD’C’ lần lượt là 2 a 2 , 3 a 2 , 6 a 2 . Tính thể tích khối hộp chữ nhật ABCD. A’B’C’D’
A. 36 a 3
B. 6 a 3
C. 36 a 6
D. 6 a 2
Cho hình chóp tứ giác đều S.ABCD có O là giao điểm của AC và BD. Biết SOasqrt{2}, góc giữa đường thẳng SA và nặt phẳng (ABCD) bằng 45o.
a) Tính thể tích khối chóp S.ABCD theo a.
b) Gọi K là điểm di động trên mặt phẳng (ABCD). Tìm widehat{SAK} để biểu thức Tdfrac{SA+AK}{SK} đạt giá trị lớn nhất.
(Giúp mình làm câu b thôi nhé.)
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có O là giao điểm của AC và BD. Biết \(SO=a\sqrt{2}\), góc giữa đường thẳng SA và nặt phẳng (ABCD) bằng 45o.
a) Tính thể tích khối chóp S.ABCD theo \(a\).
b) Gọi K là điểm di động trên mặt phẳng (ABCD). Tìm \(\widehat{SAK}\) để biểu thức \(T=\dfrac{SA+AK}{SK}\) đạt giá trị lớn nhất.
(Giúp mình làm câu b thôi nhé.)
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, BCD
120
0
và AA
7
a
2
. Hình chiếu vuông góc của A’ lên mặt phẳng ABCD trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, BCD = 120 0 và AA' = 7 a 2 . Hình chiếu vuông góc của A’ lên mặt phẳng ABCD trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.
![]()
![]()
![]()
![]()
Cho khối lập phương ABCD. A’B’C’D’ có cạnh là a. Tính thể tích khối chóp tứ giác D.ABC’D’. A.
a
3
3
B.
a
3
2
6
C.
a
3
2
3...
Đọc tiếp
Cho khối lập phương ABCD. A’B’C’D’ có cạnh là a. Tính thể tích khối chóp tứ giác D.ABC’D’.
A. a 3 3
B. a 3 2 6
C. a 3 2 3
D. a 3 4
Cho hình hộp ABCD.ABCD có O là giao điểm của AC và BD. Tỷ số thể tích của hình hộp đó và hình chóp O.ABD là:
A
.
V
A
B
C
D
.
A
B
C
D...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có O là giao điểm của AC và BD. Tỷ số thể tích của hình hộp đó và hình chóp O.A'B'D' là:
A . V A B C D . A ' B ' C ' D ' V O . A ' B ' D ' = 6
B . V A B C D . A ' B ' C ' D ' V O . A ' B ' D ' = 3
C . V A B C D . A ' B ' C ' D ' V O . A ' B ' D ' = 2
D . V A B C D . A ' B ' C ' D ' V O . A ' B ' D ' = 9