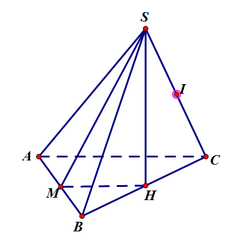
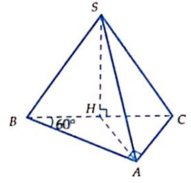
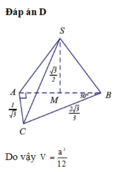
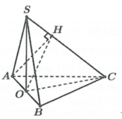
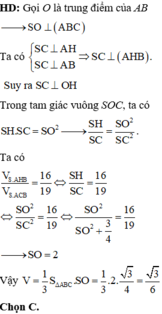
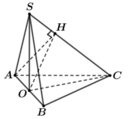
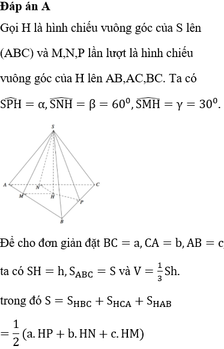
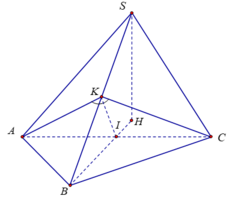
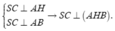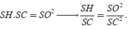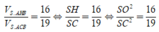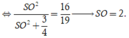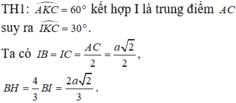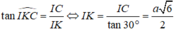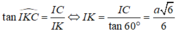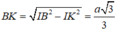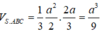Cho hình chóp S.ABC có tam giác ABC vuông tại A, AB = AC = a, I là trung điểm của SC, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm H của BC, mặt phẳng (SAB) tạo với đáy 1 góc bằng 60 0 . Tính khoảng cách từ điểm I đến mặt phẳng (SAB) theo a .

A. 3 a 5

B.  a 3 4

C.  a 3 5

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, cạnh AB = 2, A B C ^  = 60°. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Góc giữa SA và mặt phẳng đáy bằng 45°. Tính thể tích khối chóp S.ABC.

A. 4 3

B.  2 3

C. 2

D. 4 3

Cho hình chóp S.ABC có đáy là tam giác vuông tại A, A B C ^ = 30 0 , SAB là tam giác đều cạnh a, hình chiếu vuông góc của S lên mặt phẳng  (ABC) là trung điểm của cạnh AB. Thể tích của khối chóp S.ABC là:

A.  a 3 3 9

B.  a 3 18

C.  a 3 3 3

D.  a 3 12

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB=2a và B C = 2 a 3 . Gọi M là trung điểm của BC, hình chiếu vuông góc của S xuống mặt phẳng đáy là điểm  nằm trên AM thỏa mãn  A H → = 2 H M → . Góc giữa hai mặt phẳng (SAB) và (ABC) bằng 45 ° . Thể tích khối chóp S.ABC là

A.  8 a 3 3 3

B.  8 a 3 3 9

C.  8 a 3 3

D.  8 a 3 9

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy (ABC). Gọi H  là hình chiếu vuông góc của A lên SC. Biết . Thể tích của khối chóp S.ABC bằng

A.  3 2

B. 3 4

C. 3 6

D. 3 12

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy (ABC). Gọi H là hình chiếu vuông góc của A lên SC. Biết V S . A B H V S . A B C = 16 9 .  Thể tích của khối chóp S.ABC bằng

A.  3 2

B. 3 4

C. 3 6

D. 3 12

Cho hình chóp S.ABC có thể tích bằng 3 và AB=3,AC=4,BC=5. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là một điểm nằm trong tam giác ABC. Góc giữa các mặt phẳng (SAB),(SAC) và đáy lần lượt bằng 30 ° , 60 ° . Tính cotang góc giữa hai mặt phẳng (SBC) và (ABC).

A.  24 - 13 3 15

B.  8 - 5 3 5

C.  24 + 13 3 15

D.  8 + 5 3 5

Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AB = a. Gọi I là trung điểm của AC. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là điểm H thỏa mãn  B I → = 3 I H → . Góc giữa hai mặt phẳng (SAB) và (SBC) là 60 độ. Thể tích của khối chóp S.ABC là:

A. V = a³/9

B.V = a³/6

C.V = a³/18

D.V = a³/3