Thể tích khối tròn xoay gây nên bởi hình tròn x 2 + ( y − a ) 2 ≤ R 2 ( 0 < R < a ) khi quay quanh trục Ox là:
A. 8 π 2 a R 2
B. 4 π 2 a R 2
C. π 2 a R 2
D. 2 π 2 a R 2
Những câu hỏi liên quan
Thể tích khối tròn xoay gây nên bởi hình tròn
x
2
+
(
y
−
a
)
2
≤
R
2
(
0
R
a
)
khi quay quanh trục Ox là A.
8
π
2
a
R
2
B. ...
Đọc tiếp
Thể tích khối tròn xoay gây nên bởi hình tròn x 2 + ( y − a ) 2 ≤ R 2 ( 0 < R < a ) khi quay quanh trục Ox là
A. 8 π 2 a R 2
B. 8 π 2 a R 2
C. π 2 a R 2
D. 2 π 2 a R 2
Thể tích khối tròn xoay gây nên bởi hình tròn
x
2
+
(
y
-
a
)
2
≤
R
2
(
0
R
a
)
khi quay quanh trục Ox là: A.
8
π
2...
Đọc tiếp
Thể tích khối tròn xoay gây nên bởi hình tròn x 2 + ( y - a ) 2 ≤ R 2 ( 0 < R < a ) khi quay quanh trục Ox là:
A. 8 π 2 aR 2 .
B. 4 π 2 aR 2 .
C. π 2 aR 2 .
D. 2 π 2 aR 2 .
Thể tích của khối tròn xoay tạo nên do quay quanh trục Ox hình phẳng giới hạn bởi các đường y = ( 1 - x ) 2 , y = 0, x = 0 và x = 2 bằng:
Thể tích của khối tròn xoay tạo nên do quay quanh trục Ox hình phẳng giới hạn bởi các đường y
1
-
x
2
, y 0, x 0 và x 2 bằng:A.
8
π
2
3
B.
2
π...
Đọc tiếp
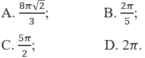
Thể tích của khối tròn xoay tạo nên do quay quanh trục Ox hình phẳng giới hạn bởi các đường y = 1 - x 2 , y = 0, x = 0 và x = 2 bằng:
A. 8 π 2 3 B. 2 π 5
C. 5 π 2 D. 2 π
Cho hình phẳng H giới hạn bởi các đường: y = f(x), y = 0, x = b và x = a (trong đó hàm số f(x) liên tục trên đoạn [b,a]). Thể tích khối tròn xoay tạo nên bởi phép quay H quanh trục Ox được cho bởi công thức:
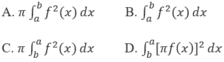
Đáp án: C.
Lưu ý ở đây b là cận dưới còn a là cận trên (b ≤ a), vậy A sai, B thiếu hệ số π, D có hệ số π 2 .
Đúng 0
Bình luận (0)
Thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường
y
1
x
−
3
,
y
0
,
x
0
,
x
2
quay một vòng quanh...
Đọc tiếp
Thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường y = 1 x − 3 , y = 0 , x = 0 , x = 2 quay một vòng quanh trục Ox là (theo đơn vị thể tích)
A. 2 π
B. 2 3 π
C. 4 3 π
D. 1 3 π
Đáp án B.
Thể tích khối tròn xoay là:
V o x = π ∫ 0 2 1 x − 3 2 d x = − π x − 3 0 2 = π − π 3 = 2 π 3
Đúng 0
Bình luận (0)
Gọi V là thể tích khối tròn xoay thành thành khi quay hình phẳng giới hạn bởi các đường
y
x
, y 0 và x 4 quanh trục Ox. Đường thẳng x a (0 a 4) cắt đồ thị hàm
y
x
tại M (hình vẽ bên). Gọi
V
1
là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng
V
2
V
1
. Khi đó: A. a...
Đọc tiếp
Gọi V là thể tích khối tròn xoay thành thành khi quay hình phẳng giới hạn bởi các đường y = x , y = 0 và x = 4 quanh trục Ox. Đường thẳng x = a (0 < a < 4) cắt đồ thị hàm y = x tại M (hình vẽ bên). Gọi V 1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V = 2 V 1 . Khi đó:
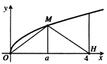
A. a = 2
B. a = 2 2
C. a = 5 2
D. a = 3
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
y
x
,
y
0
và
x
4
quanh trục Ox. Đường thẳng x a (0 a 4 cắt đồ thị hàm số
y
x
tại M (hình vẽ). Gọi V1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V2V1. Khi đó A. . B. . C. . D. .
Đọc tiếp
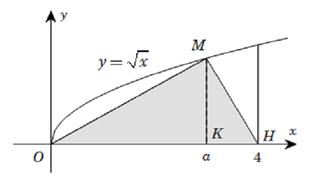
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = x , y = 0 và x = 4 quanh trục Ox. Đường thẳng x = a (0< a< 4 cắt đồ thị hàm số y = x tại M (hình vẽ). Gọi V1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V=2V1. Khi đó
A. 
.
B. 
.
C. 
.
D. 
.
Tính thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi các đường y=x^2-3x+2;y=x+2 quay quanh ox
Pt hoành độ giao điểm: \(x^2-3x+2=x+2\Leftrightarrow x^2-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
\(x^2-3x+2=0\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
\(\Rightarrow V=\pi\left(\int\limits^4_0\left(x+2\right)^2dx-\int\limits^1_0\left(x^2-3x+2\right)^2dx-\int\limits^4_2\left(x^2-3x+2\right)^2dx\right)\)
\(=\pi\left(\dfrac{208}{3}-\dfrac{5}{6}-\dfrac{14}{3}\right)=\dfrac{383\pi}{6}\)
Đúng 1
Bình luận (2)