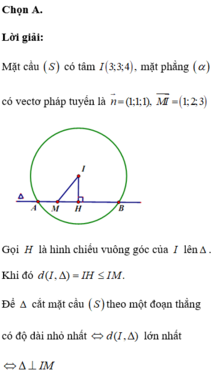
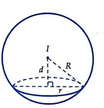
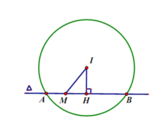
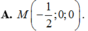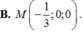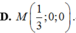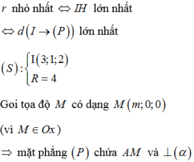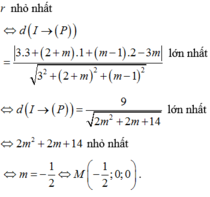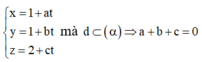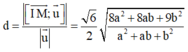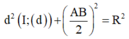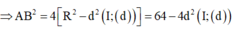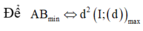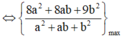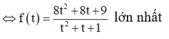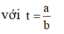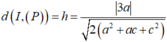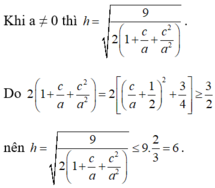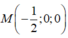Cho mặt cầu ![]() và mặt phẳng
(
α
)
:
2
x
-
2
y
-
z
+
9
=
0
.Mặt phẳng
(
α
)
cắt mặt cầu (S) theo một đường tròn (C). Tìm tọa độ tâm J và bán kính r của đường tròn (C).
và mặt phẳng
(
α
)
:
2
x
-
2
y
-
z
+
9
=
0
.Mặt phẳng
(
α
)
cắt mặt cầu (S) theo một đường tròn (C). Tìm tọa độ tâm J và bán kính r của đường tròn (C).
![]()
![]()
![]()
![]()