Nghiệm của phương trình cos 2x – 5. sin x – 3 = 0 là:
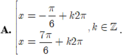
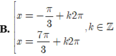
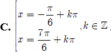
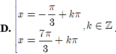
Nghiệm của phương trình cos 2 x + 3 sin x - 2 cos x = 0 là
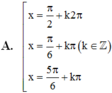
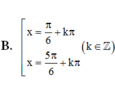
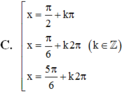
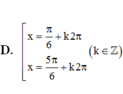
Đáp án D
Tìm điều kiện để phương trình có nghĩa. Sau đó sử dụng công thức 2 cos 2 x = 1 - 2 sin 2 x để đưa phương trình đã cho về phương trình bậc 2 đối với sin x và giải phương trình này để tìm nghiệm. Bước cuối cùng là đối chiếu điều kiện để kết luận nghiệm.
Điều kiện
![]()
Với điều kiện trên phương trình đã cho trở thành
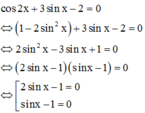
Nếu
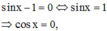
không thỏa mãn điều kiện (1)
Vậy
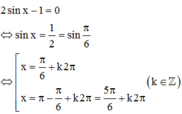
Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
Cho phương trình cos x + sin x = 1 + sin 2 x + cos 2 x . Nghiệm của phương trình có dạng x 1 = a π + k π . x 2 = ± b π + k 2 π b > 0 Tính tổng a + b
A. 1 12
B. 3
C. 7 π 12
D. π 4
Có bao nhiêu giá trị nguyên của tham số m để phương trình sin 2 x + cos 2 x + | sin x + cos x | - cos 2 x + m - m = 0 có nghiệm thực?
A. 9
B. 2
C. 3
D. 5
Đáp án C
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
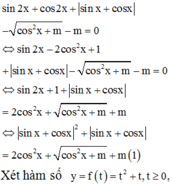
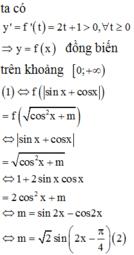

Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
nghiệm của phương trình \(1-5\sin x+2\cos^2x=0\)
Tìm số nghiệm của phương trình
cos
2
x
+
sin
x
=
0
trong khoảng ![]()
A. Vô nghiệm
B. 1
C. 2
D. 3
Gọi α là nghiệm lớn nhất của phương trình 3.cos x + cos 2x – cos 3x + 1 = 2.sin x.sin 2x thuộc khoảng 0 , 2 π . Tính sin α - π 4 .
A . - 2 2
B . 2 2
C . 0
D . 1
1. Giải các phương trình sau:
a) \(\cos\left(x+15^0\right)=\dfrac{2}{5}\)
b) \(\cot\left(2x-10^0\right)=4\)
c) \(\cos\left(x+12^0\right)+\sin\left(78^0-x\right)=1\)
2. Định m để các phương trình sau có nghiệm:
\(\sin\left(3x-27^0\right)=2m^2+m\)
c.
\(\Leftrightarrow cos\left(x+12^0\right)+cos\left(90^0-78^0+x\right)=1\)
\(\Leftrightarrow2cos\left(x+12^0\right)=1\)
\(\Leftrightarrow cos\left(x+12^0\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+12^0=60^0+k360^0\\x+12^0=-60^0+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=48^0+k360^0\\x=-72^0+k360^0\end{matrix}\right.\)
2.
Do \(-1\le sin\left(3x-27^0\right)\le1\) nên pt có nghiệm khi:
\(\left\{{}\begin{matrix}2m^2+m\ge-1\\2m^2+m\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2m^2+m+1\ge0\left(luôn-đúng\right)\\2m^2+m-1\le0\end{matrix}\right.\)
\(\Rightarrow-1\le m\le\dfrac{1}{2}\)
a.
\(\Rightarrow\left[{}\begin{matrix}x+15^0=arccos\left(\dfrac{2}{5}\right)+k360^0\\x+15^0=-arccos\left(\dfrac{2}{5}\right)+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-15^0+arccos\left(\dfrac{2}{5}\right)+k360^0\\x=-15^0-arccos\left(\dfrac{2}{5}\right)+k360^0\end{matrix}\right.\)
b.
\(2x-10^0=arccot\left(4\right)+k180^0\)
\(\Rightarrow x=5^0+\dfrac{1}{2}arccot\left(4\right)+k90^0\)
2.
Phương trình \(sin\left(3x-27^o\right)=2m^2+m\) có nghiệm khi:
\(2m^2+m\in\left[-1;1\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m^2+m\le1\\2m^2+m\ge-1\end{matrix}\right.\)
\(\Leftrightarrow\left(m+1\right)\left(2m-1\right)\le0\)
\(\Leftrightarrow-1\le m\le\dfrac{1}{2}\)
Tìm tất cả các nghiệm của phương trình cos 3x + sin 2x – sin 4x = 0
![]()
![]()
![]()
![]()