Nghiệm của phương trình 2 cos 2 x + 9 sin x - 7 = 0 là:
A. x = - π 2 + k 2 π , k ∈ Z
B. x = - π 2 + k π , k ∈ Z
C. x = π 2 + k π , k ∈ Z
D. x = π 2 + k 2 π , k ∈ Z
Những câu hỏi liên quan
Số nghiệm của phương trình
sin
x
.
sin
2
x
+
2
.
sin
x
.
cos
2...
Đọc tiếp
Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
Tổng các nghiệm thuộc đoạn [0; 3π] của phương trình 1 - 2 cos^2 x - sin x = 0 là
A. 5/3π. B. 4π. C. 6π. D. 7/2π .
\(1-2cos^2x-sinx=0\)
\(\Leftrightarrow1-2\left(1-sin^2x\right)-sinx=0\)
\(\Leftrightarrow2sin^2x-sinx-1=0\Rightarrow\left[{}\begin{matrix}sinx=1\\sinx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{\pi}{2};\dfrac{7\pi}{6};\dfrac{11\pi}{6};\dfrac{5\pi}{2}\right\}\)
\(\Rightarrow\sum x=6\pi\)
Đúng 1
Bình luận (0)
Nghiệm của phương trình
sin
x
-
3
.
cos
x
2
.
sin
3
x
là
Đọc tiếp
Nghiệm của phương trình sin x - 3 . cos x = 2 . sin 3 x là
Cho phương trình
cos
x
+
sin
x
1
+
sin
2
x
+
cos
2
x
. Nghiệm của phương trình có dạng
x
1
a
π
+
k
π
.
x
2
±
b
π
+
k
2
π
b
0
Tính tổng a + b A. ...
Đọc tiếp
Cho phương trình cos x + sin x = 1 + sin 2 x + cos 2 x . Nghiệm của phương trình có dạng x 1 = a π + k π . x 2 = ± b π + k 2 π b > 0 Tính tổng a + b
A. 1 12
B. 3
C. 7 π 12
D. π 4
Số giá trị nguyên m để phương trình
4
m
-
4
.
sin
x
.
cos
x
+
m
-
2
.
cos
2
x
3
m
-
9
. Có nghiệm là: A. 7 B. 6 C. 5 D. 4
Đọc tiếp
Số giá trị nguyên m để phương trình 4 m - 4 . sin x . cos x + m - 2 . cos 2 x = 3 m - 9 . Có nghiệm là:
A. 7
B. 6
C. 5
D. 4
Nghiệm của phương trình
cos
2
x
+
3
sin
x
-
2
cos
x
0
là
Đọc tiếp
Nghiệm của phương trình cos 2 x + 3 sin x - 2 cos x = 0 là
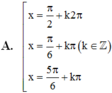
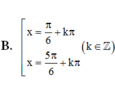
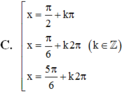
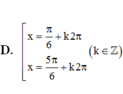
Đáp án D
Tìm điều kiện để phương trình có nghĩa. Sau đó sử dụng công thức 2 cos 2 x = 1 - 2 sin 2 x để đưa phương trình đã cho về phương trình bậc 2 đối với sin x và giải phương trình này để tìm nghiệm. Bước cuối cùng là đối chiếu điều kiện để kết luận nghiệm.
Điều kiện
Với điều kiện trên phương trình đã cho trở thành
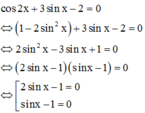
Nếu
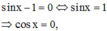
không thỏa mãn điều kiện (1)
Vậy
Đúng 0
Bình luận (0)
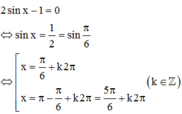
phương trình \(\cos x-\sin3x=\sqrt{2}\left(\cos x-\sin x\right)\sin4x\) có tổng tất cả các nghiệm \(x\in\left(0;\pi\right)\) là?
\(cosx-\left(3sinx-4sin^3x\right)=\sqrt{2}\left(cosx-sinx\right)sin4x\)
\(\Leftrightarrow cosx-sinx+2sinx\left(2sin^2x-1\right)=\sqrt{2}\left(cosx-sinx\right)sin4x\)
\(\Leftrightarrow cosx-sinx-2sinx\left(cosx-sinx\right)\left(cosx+sinx\right)=\sqrt{2}\left(cosx-sinx\right)sin4x\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(1-2sinx\left(sinx+cosx\right)-\sqrt{2}sin4x\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(1-2sin^2x-2sinx.cosx-\sqrt{2}sin4x\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(cos2x-sin2x-\sqrt{2}sin4x=0\right)\)
\(\Leftrightarrow\left(cosx-sinx\right)\left[sin\left(\dfrac{\pi}{4}-2x\right)-sin4x\right]=0\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
Nghiệm của phương trình
3
.
cos
x
+
sin
x
-
2
là:
Đọc tiếp
Nghiệm của phương trình 3 . cos x + sin x = - 2 là:
Trong các phương trình sau:
cos
x
5
-
3
(1);
sin
x
1
-
2
(2);
sin
x
+
cos
x
2
(3), phương trình nào vô nghiệm? A. (2) B. (1) C. (3) D. (1) và (2)
Đọc tiếp
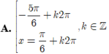
Trong các phương trình sau: cos x = 5 - 3 (1); sin x = 1 - 2 (2); sin x + cos x = 2 (3), phương trình nào vô nghiệm?
A. (2)
B. (1)
C. (3)
D. (1) và (2)
Trong các phương trình sau: cos x = 5 - 3 (1); sin x = 1 - 2 (2); sin x + cos x = 2 (3), phương trình nào vô nghiệm?
A. (2).
B. (1).
C. (3).
D. (1) và (2).
Chọn C
Ta có: 
nên (1) và (2) có nghiệm.
Cách 1:
Xét: 
nên (3) vô nghiệm.
Cách 2:
Điều kiện có nghiệm của phương trình: sin x + cos x = 2 là: 
(vô lý) nên (3) vô nghiệm.
Cách 3:
Vì 
nên (3) vô nghiệm.
Đúng 0
Bình luận (0)