Đáp án D

ĐK: sin 2 x ≠ 0 .

Khi đó:

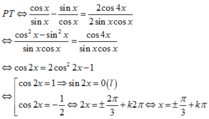
Do đó có 4 điểm x = ± π 3 ; x = 2 π 3 ; x = 4 π 3  biểu diễn nghiệm của PT đã cho.

Đáp án B

Đáp án đúng : D

\(\dfrac{sin^42x+cos^42x}{tan\left(\dfrac{\pi}{4}-x\right)tan\left(\dfrac{\pi}{4}+x\right)}=cos^4x\)

\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{cot\left(\dfrac{\pi}{4}+x\right)tan\left(\dfrac{\pi}{4}+x\right)}=cos^4x\)

\(\Leftrightarrow sin^42x+cos^42x=cos^4x\)

Giờ hạ bậc nữa là xong rồi. Làm nốt

Hình như đề bạn bị lỗi, thấy chỗ nào cũng ghi là \(cos^44x\).

ĐK: \(x\ne\dfrac{3\pi}{4}+k\pi;x\ne\dfrac{\pi}{4}+k\pi\)

\(\dfrac{sin^42x+cos^42x}{tan\left(\dfrac{\pi}{4}-x\right).tan\left(\dfrac{\pi}{4}+x\right)}=cos^44x\)

\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{\dfrac{sin\left(\dfrac{\pi}{4}-x\right)}{cos\left(\dfrac{\pi}{4}-x\right)}.\dfrac{sin\left(\dfrac{\pi}{4}+x\right)}{cos\left(\dfrac{\pi}{4}+x\right)}}=cos^44x\)

\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{\dfrac{cosx-sinx}{cosx+sinx}.\dfrac{cosx+sinx}{cosx-sinx}}=cos^44x\)

\(\Leftrightarrow sin^42x+cos^42x=cos^44x\)

\(\Leftrightarrow1-\dfrac{1}{2}sin^24x=cos^44x\)

\(\Leftrightarrow cos^44x-\dfrac{1}{2}cos^24x-\dfrac{1}{2}=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos^24x=1\\cos^24x=-\dfrac{1}{2}\left(l\right)\end{matrix}\right.\)

\(\Leftrightarrow\dfrac{1}{2}cos8x=\dfrac{1}{2}\)

\(\Leftrightarrow cos8x=1\)

\(\Leftrightarrow x=\dfrac{k\pi}{4}\)

Đối chiều điều kiện ban đầu ta được \(x=\dfrac{k\pi}{2}\)

Đáp án B

Phương trình   ⇔ 8. cos 2 x sin 2 x 1 − 3 4 sin 2 2 x = cos 2 x . sin 2 x

Điều kiện:   sin 2 x ≠ 0 ⇔ 2 x ≠ k π ⇔ x ≠ k π 2

Phương trình   ⇔ cos 2 x = 0 8 − 6 sin 2 2 x = sin 2 2 x ⇔ cos 2 x = 0 sin 2 2 x = 8 7 V N

  ⇔ 2 x = π 2 + k π ⇔ x = π 4 + k π 2 ⇒ Có 4 điểm biểu diễn trên đường tròn lượng giác.