Tìm tất cả các giá trị của tham số thực m để phương trình m 2 - 3 m + 2 x + m - 1 = 0 có nghiệm thực duy nhất.
A. m ≠ 1 m ≠ 2
B. m ≠ 1
C. m ≠ 2
D. m ≠ 1 hoặc m ≠ 2
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình x 4 - 2 x 2 - 3 + m = 0 có đúng 2 nghiệm thực
A. ( - ∞ ; 3 ) ∪ 4
B. ( - ∞ ; 3 )
C. { - 4 } ∪ ( - ∞ ; 3 )
D. ( - 3 ; + ∞ )
Tìm tất cả các giá trị thực của tham số m để phương trình 2 x 2 . 5 2 x + m = 3 có hai nghiệm.
A. m < log53 + log25
B. m > log53 + log25
C. m < log23 + log25
D. m > log53 + log35
Chọn A.
Lấy logarit cơ số 2 hai vế của phương trình, ta được ![]()
Hay x2 + (2x + m) log25 - log23 = 0
Nên x2 + 2log25.x + mlog25 - log23 = 0
Để phương trình đã cho có hai nghiệm ![]()
![]()
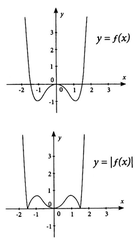
Tìm tất cả các giá trị thực của tham số m để phương trình | x 4 - 2 x 2 | = m có 3 nghiệm thực phân biệt
A. 0<m<1
B. m=0
C. m=1
D. m>1
ĐỀ THI HỌC KỲ I
Câu 1 : giải phương trình ln (3x2 - 2x +1) = ln ( 4x - 1)
Câu 2 : Tìm tập hợp các giá trị của tham số m để phương trình 3x + 3 = m \(\sqrt{9^x+1}\) có đúng 1 nghiệm
Câu 3 : Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = -x3 + 3mx + 1 có 2 điểm cực trị A , B sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ )
Tìm tất cả các giá trị thực của tham số m để phương trình 2 + 3 x + 2 - 3 x = m có nghiệm.
A. m < 5
B. m < 6
C. 2 > m
D. m ≥ 2
Tìm tất cả các giá trị thực của tham số m để bất phương trình mx^2 + (m-1)x +m -1
tìm tất cả các giá trị thực của tham số m để phương trình x-4√(x+3 ) + m = 0 có 2 nghiệm phân biệt
\(x-4\sqrt{x+3}+m=0\)
\(\Leftrightarrow x+3-4\sqrt{x+3}-3+m=0\left(1\right)\)
\(đăt:\sqrt{x+3}=t\left(t\ge0\right)\)
\(\left(1\right)\Leftrightarrow t^2-4t-3+m=0\Leftrightarrow f\left(t\right)=t^2-4t-3=-m\left(2\right)\)
\(\left(1\right)-có-2ngo-phân-biệt\Leftrightarrow\left(2\right)có-2ngo-phân-biệt-thỏa:t\ge0\)
\(\Rightarrow f\left(0\right)=-3\)
\(\Rightarrow f\left(t\right)min=\dfrac{-\Delta}{4a}=-7\Leftrightarrow t=2\)
\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)
Tìm tất cả các giá trị thực của tham số m để phương trình |f(2017x - 2018) - 2| = m có đúng 3 nghiệm
Tìm tập hợp tất cả các giá trị của tham số m để phương trình x 4 - 2 x 2 - 3 + m = 0 có đúng 2 nghiệm thực.
A. - ∞ ; 3
B. - ∞ ; 3 ∪ 4
C. - 3 ; + ∞
D. - 4 ∪ - 3 ; + ∞
tìm tất cả các giá trị thực của tham số m để phương trình \(^{x^2-2x+\sqrt{-x^2+2x}-3+m=0}\) có nghiệm
Đặt \(-x^2+2x=t\Rightarrow0\le t\le1\)
\(\Rightarrow-t^2+t-3+m=0\)
\(\Leftrightarrow t^2-t+3=m\)
Xét hàm \(f\left(t\right)=t^2-t+3\) trên \(\left[0;1\right]\)
\(-\dfrac{b}{2a}=\dfrac{1}{2}\in\left[0;1\right]\)
\(f\left(0\right)=3\) ; \(f\left(1\right)=3\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{11}{4}\)
\(\Rightarrow\dfrac{11}{4}\le f\left(t\right)\le3\)
\(\Rightarrow\) Pt có nghiệm khi và chỉ khi \(\dfrac{11}{4}\le m\le3\)