Phương trình x 4 - 10 x 2 + m = 0 có 4 nghiệm phân biệt lập thành một cấp số cộng. Khi đó m thuộc khoảng nào sau đây?
A . m ∈ 0 ; 5
B . m ∈ 5 ; 10
C . m ∈ - 5 ; 0
D . m ∈ 10 ; 15
Tìm m để phương trình \(x^4-2\left(m+1\right)x^2+2m+1=0\) có 4 nghiệm phân biệt lập thành 1 cấp số cộng
Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân: x3 – 7mx2 + 2(m2 + 6m)x – 64 = 0.
A. m = 8
B. m = 0
C. m = -1hoặc m = 7
D. m = 0 hoặc m = 8
Chọn A.
+ Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt x1; x2; x3 lập thành một cấp số nhân.
Theo định lý Vi-ét, ta có x1.x2.x3 = 64
Theo tính chất của cấp số nhân, ta có x1x3 = x22. Suy ra ta có x23 = 64 ⇔ x2 = 4
Thay x = 4 vào phương trình đã cho ta được: 43 – 7m.42 + 2(m2 + 6m).4 – 64 = 0
⇔ m2 – 8m = 0
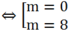
+ Điều kiện đủ: Với m = 0 thay vào phương trình đã cho ta được: x3 – 64 = 0 hay x = 4
(nghiệm kép-loại)
Với m = 8 thay vào phương trình đã cho nên ta có phương trình x3 – 56x2 + 224x – 64 = 0
Giải phương trình này, ta được 3 nghiệm phân biệt lập thành cấp số nhân.
Vậy m = 8 là giá trị cần tìm.
Giá trị của m để phương trình có ba nghiệm phân biệt lập thành một cấp số cộng x 3 - 3 x 2 + x - m = 0 thuộc khoảng nào trong các khoảng dưới đây?
A.(2;4)
B.(-2;0)
C.(0;2)
D.(-4;2)
Giá trị của m để phương trình x 3 - 3 x 2 + x - m = 0 có ba nghiệm phân biệt lập thành một cấp số cộng thuộc khoảng nào trong các khoảng dưới đây?
A. (2;4).
B. (-2;0).
C. (0;2).
D. (-4;2).
Chọn B.
Xét hàm số f(x) =
x
3
-
3
x
2
+
x
-
m
, ![]()
![]()
Điểm uốn của đồ thị hàm số là A (1;-1-m).
Phương trình x 3 - 3 x 2 + x - m = 0 có ba nghiệm phân biệt lập thành một cấp số cộng.
![]()
Bài 1: Tìm m để phương trình sau có 3 nghiệm lập thành 1 cấp số cộng:
1, \(x^3-x^2-m^2x+m^2=0\)
2, \((x-2)(x^2-2mx+2m+3)=0\)
3, \(x^3-(2m-3)x^2-mx+m-2=0\)
4, \(x^3+(2m-1)x^2+(4m+1)x+2m+3=0\)
Bài 2: Tìm m để phương trình sau có 4 nghiệm lập thành 1 cấp số cộng:
a, \(-x^4+2mx^2-2m+1=0\)
b, \(x^4+2(m-2)x^2+m^2-5m+5=0\)
Bài 3: Tìm 3 số lập thành 1 cấp số cộng biết tổng của chúng bằng tổng các bình phương bằng 83
Tổng tất cả các giá trị của m để phương trình x 4 - 2 ( m + 1 ) x 2 + 2 m + 1 = 0 có 4 nghiệm phân biệt lập thành cấp số cộng là
A. 14 9
B. 32 9
C. 17 3
D. 19 3
Có bao nhiêu giá trị thực của tham số m để phương trình ( x - 1 ) ( x - 3 ) ( x - m ) = 0 có 3 nghiệm phân biệt lập thành cấp số nhân tăng?
A. 2
B. 1
C. 4
D. 3
Có bao nhiêu giá trị thực của tham số m để phương trình ( x - 1 ) ( x - 3 ) ( x - m ) = 0 có 3 nghiệm phân biệt lập thành cấp số nhân tăng?
A. 2
B. 1
C. 4
D. 3
Chọn đáp án D
Phương pháp
Cho ba số a, b, c lập thành CSN thì ta có: b 2 = a c .
Cách giải
Ta có: ( x - 1 ) ( x - 3 ) ( x - m ) = 0
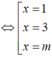
Phương trình đã cho có 3 nghiệm phân biệt
![]()
+) Giả sử 1; 3; m lập thành 1 CSN tăng
![]()
+) Giả sử m; 1; 3 lập thành 1 CSN tăng
![]()
+) Giả sử 1; m; 3 lập thành 1 CSN tăng
![]()
Vậy có 3 giá trị m thỏa mãn
Cho phương trình \(x^4+3x^2-\left(24+m\right)x-26-n=0\), tìm hệ thức liên hệ giữa m và n để 3 nghiệm phân biệt \(x_1,x_2,x_3\) lập thành một cấp số cộng ?
Vì 3 nghiệm phân biệt : \(x_1,x_2,x_3\) lập thàng cấp số cộng, nên ta có thể đặt :
\(x_1=x_0-d,x_2=x_0;x_3=x_0+d\left(d\ne0\right)\). Theo giả thiết ta có :
\(x^3+3x^2-\left(24+m\right)x-26-n=\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\)
\(=\left(x-x_0+d\right)\left(x-x_0\right)\left(x-x_0-d\right)\)
\(=x^3-3x_0x^2+\left(3x^2_0-d^2\right)x-x^3_0+x_0d^2\) với mọi x
Đồng nhất hệ số ở hai vế của phương trình ta có hệ :
\(\begin{cases}-3x_0=3\\3x_0^2-d^2=-\left(24+m\right)\\-x_0^3+x_0d^2=-26-n\end{cases}\) \(\Leftrightarrow\begin{cases}x_0=-1\\3-d^2=-24-m\\1-d^2=-26-n\end{cases}\) \(\Leftrightarrow\begin{cases}x_0=-1\\m=n\end{cases}\)
Vậy với m = n thì 3 nghiệm phân biệt của phương trình lập thành cấp số cộng