Số 1458 là số hạng thứ bao nhiêu của cấp số nhân ( u n ) có công bội u 1 = 2 v à q = 3
A. 8
B. 5
C. 6
D. 7
Số 1458 là số hạng thứ bao nhiêu của cấp số nhân u n có số hạng đầu u 1 = 2 và công bội q = 3
A. 8
B. 5
C. 6
D. 7
Số 1458 là số hạng thứ bao nhiêu của cấp số nhân (un) có công bội u1=2 và q=3
A. 8
B. 5
C. 6
D. 7
Cho cấp số nhân \(\left( {{u_n}} \right)\) với số hạng đầu \({u_1} = - 5\), công bội q = 2
a) Tìm \({u_9}\)
b) Số \( - 320\) là số hạng thứ bao nhiêu của cấp số nhân?
c) Số 160 có phải là một số hạng của cấp số nhân trên không?
a) \({u_9} = {u_1}.{q^{9 - 1}} = \left( { - 5} \right){.2^8} = - 1280\)
b) Ta có: \( - 320 = \left( { - 5} \right){.2^{n - 1}} \Leftrightarrow {2^{n - 1}} = 64 \Leftrightarrow n = 7\)
\( - 320\) là số hạng thứ 7 của cấp số nhân
c) Ta có: \(160 = \left( { - 5} \right){.2^{n - 1}} \Leftrightarrow {2^{n - 1}} = - {2^5}\)
160 không là số hạng của cấp số nhân
Cho cấp số nhân có số hạng đầu bằng 1, công bội bằng 3. Hỏi số hạng thứ 2018 của cấp số đó là một số tự nhiên có bao nhiêu chữ số?
Cấp số nhân ( u n ) có u 1 + u 5 = 51 u 2 + u 6 = 102
a) Tìm số hạng đầu và công bội của cấp số nhân:
b) Hỏi tổng của bao nhiêu số hạngđầu tiên sẽ bằng 3096?
c) Số 12288 là số hạng thứ mấy?
a ) u 1 = 3 , q = 2 b ) n = 10 c ) n = 13
Một cấp số nhân với công bội bằng −2, có số hạng thứ ba bằng 8 và số hạng cuối bằng −1024. Hỏi cấp số nhân đó có bao nhiêu số hạng?
A. 11.
B. 10.
C. 9.
D. 8.
Một cấp số nhân hữu hạn u n có công bội bằng -2 số hạng thứ 3 bằng 8 và số hạng cuối bằng -1024. Cấp số nhân đã cho có bao nhiêu số hạng
A. 11
B. 10
C. 12
D. 8
Có 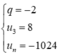
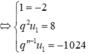
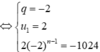
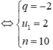
Cấp số nhân đã cho có 10 số hạng.
Chọn đáp án B.
Chỉ cần đáp án thôi ạ, mình cần gấp ạ
Một cấp số nhân với công bội bằng -2, có số hạng thứ ba bằng 8 và số hạng cuối bằng -1024. Hỏi cấp số nhân đó có bao nhiêu số hạng?
A. 10
B. 11
C. 8
D. 9
Nếu cấp số nhân có công bội q = 1 thì tổng n số hạng đầu \(S_n\) của nó bằng bao nhiêu?
Nếu cấp số nhân có công bội q = 1 thì cấp số nhân là \(u_1, u_1, ..., u_1,...\) Khi đó
\({S_n} = u_1 + u_1 + ... + u_1 = n . u_1\) (tổng của n số hạng u_1).