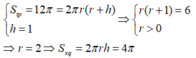Diện tích xung quanh của một hình trụ là 10 m 2 và diện tích toàn phần của nó là 14 m 2 .Hãy tính bán kính của đường tròn đáy và chiều cao của hình trụ (lấy π =3,14 ; làm tròn kết quả đến chữ số thập phân thứ 2)

Những câu hỏi liên quan
Một hình chữ nhật ABCD có AB > AD, diện tích và chu vi của nó theo thứ tự là 2 a 2 và 6a. Cho hình vẽ quay xung quanh cạnh AB ta được một hình trụ. Tính diện tích toàn phần và thể tích của hình trụ này
Ta có: S t p = 2 πBC . AB + 2 πBC 2 = 2 π . 2 a . a + 2 πa 2 = 6 πa 2
Ta có: V = π . BC 2 . AB = πa 2 . 2 a = 2 πa 3
Đúng 0
Bình luận (0)
Một hình trụ có diện tích xung quanh là 140𝜋 cm2 và diện tích toàn phần của hình trụ là 360𝜋 cm2 . Tính bán kính đáy của hình trụ.
\(S_{xq}=140\pi\Leftrightarrow2\pi rh=140\pi\Leftrightarrow h=\dfrac{70}{r}\left(1\right)\)
\(S_{tp}=360\pi\Leftrightarrow2\pi r\left(r+h\right)=360\pi\Leftrightarrow r\left(r+h\right)=180\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow r\left(r+\dfrac{70}{r}\right)=180\\ \Leftrightarrow r^2+70=180\Rightarrow r=\sqrt{110}\)
Đúng 3
Bình luận (0)
Tổng diện tích 2 đáy là:
\(360\pi-140\pi=220\pi\left(cm^2\right)\)
Bán kính đáy hình trụ là:
\(\sqrt{\dfrac{220\pi}{2\pi}}=\sqrt{110}\) (cm2)
Đúng 1
Bình luận (0)
Một khối gỗ hai đầu chênh lệch không đáng kể được coi như một hình trụ có đáy là hình tròn có chiều dài 3,5 m chiều dài chính là chiều cao của hình trụ có đường kính bằng 0,7 m. Tính
a. Diện tích xung quanh và diện tích toàn phần của khúc gỗ
b. Tính thể tích cua rkhucs gỗ
Cho hình trụ có diện tích toàn phần là 12π, đường cao của hình trụ là 1. Diện tích xung quanh của hình trụ là:
A. 6π
B. 4π
C. 2π
D. π
a, một lăng trụ đứng có đáy là một tam giác vuông, các cạnh hóc vuông của tam giác vuông là 3cm, 4cm. chiều cao của hình lăng trụ là 9cm.tính thể tích và diện tích xung quanh, diện tích toàn phần của lăng trụ
b, một lăng trụ đứng có đáy là hình chữ nhật có các kích thước là 3cm, 4cm. chiều cao của lăng trụ là 5cm. tính diện tích xung quanh của lăng trụ
a. Thể tích là:
\(\frac{3x4}{2}\)x 9 = 54 cm3
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}\) = 5 cm
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
Đúng 2
Bình luận (0)
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2
Đúng 3
Bình luận (0)
a. Thể tích là:
\(\dfrac{3x4}{2}\times9=54cm^3\)
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}5cm\)
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2
Đúng 1
Bình luận (0)
Một hình trụ có bán kính đáy là 3cm. Biết diện tích toàn phần của hình trụ gấp đôi diện tích xung quanh. Tính chiều cao của hình trụ
Diện tích toàn phần gấp đôi diện tích xung quanh nên:
2πRh + 2π R 2 = 2.2π R 2 => 2πRh = 2π R 2 => R = h
Vậy chiều cao của hình trụ là 3cm
Đúng 0
Bình luận (0)
Diện tích xung quanh của một hình trụ là \(10cm^2\) và diện tích toàn phần của nó là \(14m^2\). Hãy tính bán kính của đường tròn đáy và chiều cao của hình trụ (lấy \(\pi\approx3,14\), làm tròn kết quả đến chữ số thập phân thứ hai)
Một hình lăng trụ đứng có đáy là một tam giác vuông. Độ dài hai cạnh góc vuông của đáy là 3cm và 4cm. Chiều cao của lăng trụ là 8cm. Hãy tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lăng trụ đó.
Áp dụng định lí Py - Ta - Go , độ dài cạnh còn lại của mặt đáy tam giác là :
\(\sqrt{3^2+4^2}=5\left(cm\right)\)
Diện tích xung quanh hình lăng trụ đứng :
\(S_{xq}=\left(3+4+5\right).8=96\left(cm^2\right)\)
Diện tích toàn phần :
\(S_{tp}=96+\left(3.4\right)=108\left(cm^2\right)\)
Thể tích :
\(V=\dfrac{3.4}{2}.8=48\left(cm^3\right)\)
Đúng 2
Bình luận (0)
Phần tự luận
Cho hình trụ có đường sinh bằng 10 cm và diện tích xung quanh của hình trụ bằng 160π ( c m 2 ). Tính:
a) Diện tích toàn phần của hình trụ.
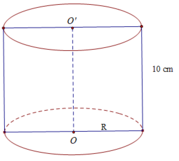
a) Ta có:
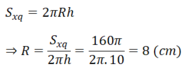
Diện tích đáy: S đ á y = π R 2 = π. 8 2 = 64π ( c m 2 )
Diện tích toàn phần: S t p = S x q + 2 S đ á y = 160π + 2.64π = 288π ( c m 2 )
Đúng 0
Bình luận (0)