Phương trình
c
o
t
x
+
3
0
có các nghiệm là
Đọc tiếp
Phương trình c o t x + 3 = 0 có các nghiệm là
Những câu hỏi liên quan
Các khẳng định sau đây đúng hay sai:a. Phương trình
4
x
-
8
+
4
-
2
x
x
2
+
1
0
có nghiệm x 2.b. Phương trình ...
Đọc tiếp
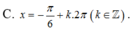
Các khẳng định sau đây đúng hay sai:
a. Phương trình 4 x - 8 + 4 - 2 x x 2 + 1 = 0 có nghiệm x = 2.
b. Phương trình x + 2 2 x - 1 - x - 2 x 2 - x + 1 = 0 có tập nghiệm S = {-2; 1}
c. Phương trình x 2 + 2 x + 1 x + 1 = 0 có nghiệm x = - 1
d. Phương trình x 2 x - 3 x = 0 có tập nghiệm S = {0; 3}
a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình 
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 
Đúng 0
Bình luận (0)
cho a,b,c là các số dương đôi một khác nhau có tổng là 12.CMR trong ba phương trình sau có một phương trình vô nghiệm 1 phương trình có nghiệm
(1) x2+ax+b=0
(2)x2+bx+c=0
(3)x2+cx+a=0
Cho các khẳng định sau:(1) Phương trình |x – 3| 1 chỉ có một nghiệm là x 2(2) Phương trình |x – 1| 0 có 2 nghiệm phân biệt(3) Phương trình |x – 3| 1 có hai nghiệm phân biệt là x 2 và x 4Số khẳng định đúng là: A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Cho các khẳng định sau:
(1) Phương trình |x – 3| = 1 chỉ có một nghiệm là x = 2
(2) Phương trình |x – 1| = 0 có 2 nghiệm phân biệt
(3) Phương trình |x – 3| = 1 có hai nghiệm phân biệt là x = 2 và x = 4
Số khẳng định đúng là:
A. 0
B. 1
C. 2
D. 3
Xét phương trình |x – 3| = 1
TH1: |x – 3| = x – 3 khi x – 3 ≥ 0 ó x ≥ 3
Phương trình đã cho trở thành x – 3 = 1 ó x = 4 (TM)
TH2: |x – 3| = 3 – x khi x – 3 < 0 ó x < 3
Phương trình đã cho trở thanh 3 – x = 1 ó x = 2 (TM)
Vậy phương trình |x – 3| = 1 có hai nghiệm x = 2 và x = 4 hay (1) sai và (3) đúng
|x – 1| = 0 ó x – 1 = 0 ó x = 1 nên phương trình |x – 1| = 0 có nghiệm duy nhất hay (2) sai.
Vậy có 1 khẳng định đúng
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Trong các khẳng định sau, số khẳng định đúng là:a) Tập nghiệm của phương trình
x
2
+
3
x
x
0
là {0; 3}b) Tập nghiệm của phương trình
x
2
-
4
x
-
2...
Đọc tiếp
Trong các khẳng định sau, số khẳng định đúng là:
a) Tập nghiệm của phương trình x 2 + 3 x x = 0 là {0; 3}
b) Tập nghiệm của phương trình x 2 - 4 x - 2 = 0 là {-2}
c) Tập nghiệm của phương trình x - 8 x - 7 = 1 7 - x + 8 là {0}
A. 1
B. 2
C. 0
D. 3
Cho phương trình \(x^2-\left(2m+3\right)x+m=0\)
a) Chứng minh rằng phương trình đã cho có nghiệm với mọi m.
b) goi x1,x2
là các nghiệm của phương trình. tìm m để T=\(x_1^2+x_2^2\) đạt giá trị nhỏ nhất.
a,\(\Delta=\left[-\left(2m+3\right)\right]^2-4m=4m^2+12m+9-4m=4m^2+8m+9\)\(=\)\(4\left(m^2+2m+\dfrac{9}{4}\right)=4\left(m+1\right)^2+5\ge5>0\)
=>pt luôn có 2 nghiệm phân biệt
b,vi ét \(=>\left\{{}\begin{matrix}x1+x2=2m+3\\x1x2=m\end{matrix}\right.\)
\(T=\left(x1+x2\right)^2-2x1x2=\left(2m+3\right)^2-2m=4m^2+12m+9-2m\)\(=4m^2+10m+9=4\left(m^2+\dfrac{10}{4}m+\dfrac{9}{4}\right)=4\left[\left(m+\dfrac{5}{4}\right)^2+\dfrac{11}{16}\right]\)\(=4\left(m+\dfrac{5}{4}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\)
dấu"=" xảy ra<=>m=-5/4
Đúng 3
Bình luận (0)
Họ nghiệm của phương trình tan(x+frac{pi}{5})+ sqrt{3} 0 là?Phương trình tanx tanx/2 có họ nghiệm là?Nghiệm của phương trình √3 + 3tanx 0 có nghiệm là?Phương trình √3 + tanx 0 có nghiệm là?Họ nghiệm của phương trình tan2x - tanx 0 là?Phương trình lượng giác 3cotx - √3 0 có nghiệm là?Pt lượng giác 2cotx - √3 0 có nghiệm là?
Đọc tiếp
Họ nghiệm của phương trình tan(x+\(\frac{\pi}{5}\))+ \(\sqrt{3}\)= 0 là?
Phương trình tanx= tanx/2 có họ nghiệm là?
Nghiệm của phương trình √3 + 3tanx =0 có nghiệm là?
Phương trình √3 + tanx = 0 có nghiệm là?
Họ nghiệm của phương trình tan2x - tanx = 0 là?
Phương trình lượng giác 3cotx - √3 = 0 có nghiệm là?
Pt lượng giác 2cotx - √3 = 0 có nghiệm là?
Cho a,b,c là 3 số phân biệt sao cho các phương trình: x2+ax+1=0 và x2+bx+c=0 có nghiệm chung. Đồng thời các phương trình x2+x+a=0 và x2+cx+b=0 cũng có nghiệm chung.
Tính giá trị của biểu thức P=a+b+c
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+30 và ( a+1)x-a+202/ Bất phương trình: 5x/5 - 13/21 + x/15 9/25- 2x/35 có nghiệm là....3/ Bất phương trình: 5x-1 2x/5 + 3 có nghiệm là...4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) (4x/3x-x^2) có nghiệm nguyên lớn nhất là...5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 2x -166/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 12 - 2x/37/ Bất phương trình: 2(x-1) - x 3(x-1) - 2x-5 có t...
Đọc tiếp
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Xem thêm câu trả lời
27 tháng 8 2020 lúc 21:04
Cho a,b,c là các số dương đôi một khác nhau sao cho a+b+c = 12. CMR trong 3 phương trình sau có 1 phương trình có nghiệm, một phương trình vô nghiệm:
\(x^2+ax+b=0\); \(x^2+bx+c=0\); \(x^2+cx+a=0\)
Ta có:
\(\Delta_1+\Delta_2+\Delta_3=a^2-4b+b^2-4c+c^2-4a=a^2+b^2+c^2-48\)
Dễ thấy:\(a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3}=48\Rightarrow\Delta_1+\Delta_2+\Delta_3\ge0\)
Khi đó có ít nhất một phương trình có nghiệm
còn c/m vô nghiệm thế nào z
Cho a,b,c là các số thực dương phân biệt có tổng bằng 3. Chứng minh rằng trong ba phương trình \(x^2-2ax+b=0;x^2-2bx+c;x^2-2cx+a=0\)
có ít nhất một phương trình có hai nghiệm phân biệt và ít nhất một phương trình vô nghiệm
* Giả sử cả 3 pt đều có nghiệm kép hoặc vô nghiệm ta có :
pt \(x^2-2ax+b=0\) (1) có \(\Delta_1'=\left(-a\right)^2-b=a^2-b\le0\)
pt \(x^2-2bx+c=0\) (2) có \(\Delta_2'=\left(-b\right)^2-c=b^2-c\le0\)
pt \(x^2-2cx+a=0\) (3) có \(\Delta_3'=\left(-c\right)^2-a=c^2-a\le0\)
\(\Rightarrow\)\(\Delta_1'+\Delta_2'+\Delta_3'=\left(a^2+b^2+c^2\right)-\left(a+b+c\right)\le0\) (*)
Lại có : \(0< a,b,c< 3\)\(\Rightarrow\)\(\hept{\begin{cases}a\left(3-a\right)>0\\b\left(3-b\right)>0\\c\left(3-c\right)>0\end{cases}\Leftrightarrow\hept{\begin{cases}3a>a^2\\3b>b^2\\3c>c^2\end{cases}}}\)
\(\Rightarrow\)\(\left(a^2+b^2+c^2\right)-\left(a+b+c\right)< 3\left(a+b+c\right)-\left(a+b+c\right)=2\left(a+b+c\right)=6>0\)
trái với (*)
Vậy có ít nhất một phương trình có hai nghiệm phân biệt
cái kia chưa bt làm -_-
Đúng 1
Bình luận (0)
nhầm r >_< sửa lại chỗ này nhé
Lại có : \(0< a,b,c< 3\)\(\Rightarrow\)\(\hept{\begin{cases}a\left(3-a\right)< 0\\b\left(3-b\right)< 0\\c\left(3-c\right)< 0\end{cases}\Leftrightarrow\hept{\begin{cases}3a< a^2\\3b< b^2\\3c< c^2\end{cases}}}\)
\(\Rightarrow\)\(\left(a^2+b^2+c^2\right)-\left(a+b+c\right)>3\left(a+b+c\right)-\left(a+b+c\right)=6>0\) :))
Đúng 1
Bình luận (0)