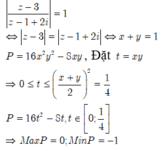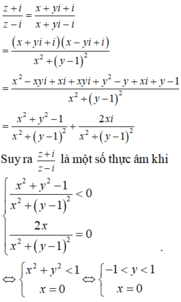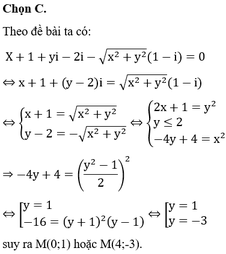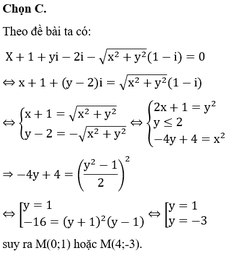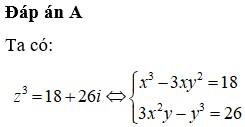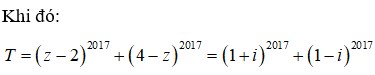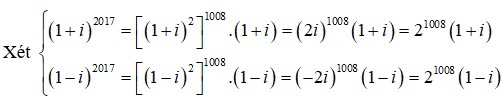Cho số phức z = x + y i với x, y là các số thực không âm thỏa mãn z - 3 z - 1 + 2 i và biểu thức P = z 2 - z - 2 + i z 2 - z - 2
z 1 - i + z - 1 + i . Giá trị lớn nhất và giá trị
nhỏ nhất của P lần lượt là:
A. 0 và - 1
B. 3 và - 1
C. 3 và 0
D. 2 và 0
Cho số phức z = x + yi. Tập hợp các điểm biểu diễn của số phức z sao cho số phức z + i z - i là một số thực âm là:
A. Các điểm trên trục hoành với -1<x<1
B. Các điểm trên trục tung với -1<y<1
C. Các điểm trên trục tung với - 1 ≤ y < 1
D. Các điểm trên trục tung với y ≤ - 1 y ≥ 1
Cho x,y,z là các số thực không âm thỏa mãn x+y+z=3 . Tìm GTNN và GTLN của biểu thức N = căn(x+y) + căn(y+z) + căn(x+z)
Cho x, y, z là các số thực không âm thỏa mãn x + y + z = 3. Chứng minh bất đẳng thức: (1 - x)^3 + (1 - y)^3 + (1 - z)^3 ≤ 3/4
có: \(x\left(2x-3\right)^2\ge0\Leftrightarrow4x^3-12x^2+9x\ge0\Leftrightarrow4x^3-12x^2+12x-4\ge3x-4\)
\(\Leftrightarrow4\left(x-1\right)^3\ge3x-4\)
\(\Leftrightarrow\left(1-x\right)^3\le1-\frac{3}{4}x\).
tương tự và cộng lại ta có ngay đpcm.
Dấu = xảy ra khi 2 số bằng 1,5; 1 số bằng 0
Cho x,y,z là các số thực không âm thỏa mãn x+y+z=1. Tìm GTLN của biểu thức A = -z^2+z(y+1)+xy
Cho số phức z=x+yi (x,y∈ R) thỏa mãn z+1-2i- z (1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây?
A. x+y-2=0.
B. x-y+2=0.
C. x+y-1=0.
D. x+y+1=0.
Cho số phức z=x+yi (x,y∈ R) thỏa mãn z+1-2i- z (1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây?
A. x+y-2=0.
B. x-y+2=0.
C. x+y-1=0.
D. x+y+1=0.
cho x,y,z là các số thực không âm thỏa mãn x^3+y^3+z^3 =3
tìm Min P= x^3/3y+1 + y^3/3z+1 + z^3/3x+1
GIÚP MK VỚI Ạ
Chị tham khảo bài giải dưới đây nhé:
x^3/(3y+1) +(3y+1)/16+1/4 \(\ge\)3 . căn bậc 3\(\sqrt[]{\frac{x^3.\left(3y+1\right).1}{\left(3y+1\right).16.4}}\)\(\ge\)3x/4(BĐT cauchy) (1)
y^3/(3z+1)+(3z+1)/16+1/4 \(\ge\)3. căn bậc 3\(\sqrt[]{\frac{z^3.\left(3z+1\right).1}{\left(3z+1\right).16.4}}\)\(\ge\)3y/4 (BĐT cauchy) (2)
z^3/(3x+1) +(3x+1)/16 +1/4 \(\ge\) 3. \(\sqrt[3]{\frac{z^3.\left(3x+1\right).1}{\left(3y+1\right).16.4}}\)\(\ge\)3z/4(BĐT cauchy) (3)
cộng theo vế của các bất đảng thức (1),(2),(3) ta có BĐT tương đương
P+3(x+y+z)/16+3/16 \(\ge\)3(x+y+z)/4
\(\Leftrightarrow\)P+3/16\(\ge\)3(x+y+z)/4 -3(x+y+z)/16=9(x+y+z)/16\(\ge\)9/16
\(\Rightarrow\)P+3/16\(\ge\)9/16
\(\Leftrightarrow\)P\(\ge\)3/16
vậy min P=3/16 . Dấu "=" xảy ra khi và chỉ khi x=y=z=1
Chị Linh Mai ơi em không học lớp 9 nhưng bài này có thể em biết làm . Và bài giải trên chỉ mang tính tham khảo thôi nha chị , chưa chắc đúng đâu . Chị cần tham khỏa các bài khác coi đúng không nhé! Em chúc chị mai thi tuyển sinh làm bài tốt nha!
bạn kia giải sai rồi
Cho số phức z=x+yi, ( x , y ∈ R ) thỏa mãn z 3 = 18 + 26 i . Tính T = ( z - 2 ) 2017 + ( 4 - z ) 2017
A. T = 2 1009
B. T = 2 1010
C. T = 2 1011
D. T = 2 2012
