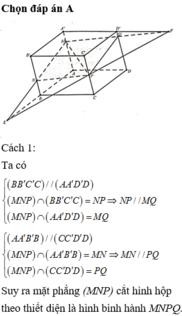
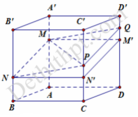
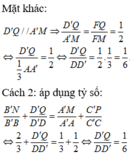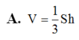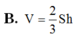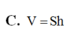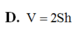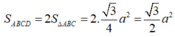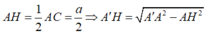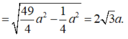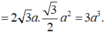Cho hình hộp ABCD.A'B'C'D' Trên các cạnh AA’; BB’; CC’ lần lượt lấy ba điểm M, N, P sao cho 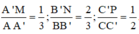 Biết mặt phẳng (MNP) cắt cạnh DD’ tại Q. Tính tỉ số
D
'
Q
D
D
'
Biết mặt phẳng (MNP) cắt cạnh DD’ tại Q. Tính tỉ số
D
'
Q
D
D
'
A. 1 6
B. 1 4
C. 3 8
D. 2 9