Trong không gian toạ độ Oxyz cho 3 điểm A 0 ; 2 ; 1 ; B 1 ; 0 ; 2 ; C 2 ; 1 ; − 3 . Tập hợp các điểm thoã mãn M A 2 + M B 2 + M C 2 = 20 là một mặt cầu. Bán kính mặt cầu đó là.
A. R = 2
B. R = 6 2
C. R = 6 3
D. R = 2 5
Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng P : 6 x + 3 y - 2 z + 24 = 0 và điểm A(2;5;1). Tìm toạ độ hình chiếu vuông góc H của A trên (P).
A. H(4;2;3)
B. H(4;2;-3)
C. H(4;-2;3)
D. H(-4;2;3)
Đáp án D.
Mặt phẳng (P) có 1 vecto pháp tuyến n → = ( 6 ; 3 ; - 2 )
Đường thẳng AH qua A và vuông góc vưới (P)
Suy ra phương trình của đường thẳng AH là
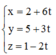
Suy ra H(2+6t; 5+3t; 1-2t)
Mà

Vậy H(-4;2;3)
Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng P : 6 x + 3 y - 2 z + 24 = 0 và điểm A(2;5;1). Tìm toạ độ hình chiếu vuông góc H của A trên (P).
A. H(4;2;3)
B. H(4;2;-3)
C. H(4;-2;3)
D. H(-4;2;3)
Đáp án D.
Mặt phẳng (P) có 1 vecto pháp tuyến n → = ( 6 ; 3 ; - 2 )
Đường thẳng AH qua A và vuông góc vưới (P)
Suy ra phương trình của đường thẳng AH là

Suy ra H(2+6t; 5+3t; 1-2t)
Mà

Vậy H(-4;2;3)
Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P):6x + 3y - 2z + 24 = 0 và điểm A(2;5;l). Tìm toạ độ hình chiếu vuông góc H của A trên (P).
A. H(4; 2; 3)
B. H(4; 2; -3)
C. H(4; -2; 3)
D. H(-4; 2; 3)
Trong không gian với hệ toạ độ Oxyz, cho 3 điểm M(3;0;0), N(0;-2;0), P(0;0;1). Mặt phẳng (MNP) có phương trình:
![]()
![]()
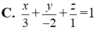
![]()
Đáp án C
Ta có M,N,P lần lượt là giao điểm của (MNP) với 3 trục tọa độ
![]()
Trong không gian toạ độ Oxyz, cho mặt phẳng (P): x-2y+z-3=0 và điểm A(1;2;0). Viết phương trình đường thẳng qua A và vuông góc với (P).
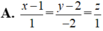
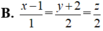
![]()
![]()
Đáp án A
Mặt phẳng (P) có véc-tơ pháp tuyến là ![]() =(1;-2;1) nên đường thẳng cần tìm có véc-tơ chỉ phương là
=(1;-2;1) nên đường thẳng cần tìm có véc-tơ chỉ phương là ![]() =(1;-2;1).
=(1;-2;1).
Vậy phương trình đường thẳng đi qua A và vuông góc với (P) là ![]()
Trong không gian với hệ toạ độ Oxyz, cho điểm A(2;3;4). Khoảng cách từ A đến trục toạ độ Ox bằng
A. 2.
B. 4.
C. 3.
D. 5.
Trong không gian Oxyz, cho hai điểm A(1;−2;1), B(0;1;−3). Toạ độ véctơ A B ⇀ là
A. (1;-3;4)
B. (1;-1;2)
C. (-1;3;-4)
D. (-1;1;2)
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2; -3; 2), B (3; 5; 4). Tìm toạ độ điểm M trên trục ?z sao cho MA2 + MB2 đạt giá trị nhỏ nhất.
A. M (0; 0; 49)
B. M (0; 0; 67)
C. M (0; 0 ;3)
D. M (0; 0; 0)
Chọn C
Gọi I là trung điểm của AB 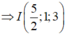
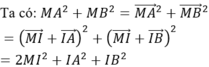
Suy ra: MA2 + MB2 đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
=>M là hình chiếu của I trên trục Oz => M (0 ; 0 ; 3)
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2; -3; 2), B (3; 5; 4). Tìm toạ độ điểm M trên trục Oz sao cho M A 2 + M B 2 đạt giá trị nhỏ nhất.
A. M (0; 0; 49).
B. M (0; 0; 67)
C. M (0; 0 ;3)
D. M (0; 0; 0)
Trong không gian với hệ toạ độ Oxyz, cho điểm M(4;3;2). Có bao nhiêu mặt phẳng qua M cắt ba trục toạ độ Ox,Oy,Oz lần lượt tại A,B,C sao cho 6OA=2OB=3OC>0.
A. 8.
B. 1.
C. 3.
D. 4.