Một hình đa diện, mệnh đề nào dưới đây đúng?
A. Hai mặt bất kì có ít nhất một điểm chung
B. Hai mặt bất kì có ít nhất một cạnh chung
C. Hai cạnh bất kì có ít nhất một điểm chung
D. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt
Những câu hỏi liên quan
Cho một hình đa diện. Khẳng định nào sau đây là sai?
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C. Mỗi đỉnh là cạnh chung của ít nhất ba mặt.
D. Mỗi mặt có ít nhất ba cạnh.
Chọn C.
Dựa vào định nghĩa khối đa diện. Mỗi cạnh là cạnh chung của đúng hai mặt.
Đúng 0
Bình luận (0)
Trong bảng ô vuông kích thước 8x8 gồm 64 ô vuông đơn vị, người ta đánh dấu 13 ô bất kì. Chứng minh rằng với mọi cách đánh dấu luôn có ít nhất 4 ô được đánh dấu không có điểm chung ( hai ô có điểm chung là hai ô chung cạnh hoặc chung đỉnh)
Trong bảng ơi vuông kích thước 8x8 gồm 64 ơi vuông đơn vị , người ta đánh dấu 13 ơi bất kì .Chứng minh với mọi cách đánh dấu luôn có ít nhất 4 ô được đánh dấu. không có điểm chung ( 2 ơi có điểm chung là hai ô có chung đỉnh hoặc sư chung cạnh)
Giải mục 1 trang 113, 114 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 20:28
Hộp giấy có các mặt là hình vuông ở Hình 1a được vẽ lại với các đỉnh là \(A,B,C,D,A',B',C',D'\) như Hình 1b. Gọi tên cặp mặt phẳng:
a) Có ba điểm chung không thẳng hàng.
b) Là hai mặt phẳng phân biệt và có một điểm chung.
c) Không có bất kì điểm chung nào.
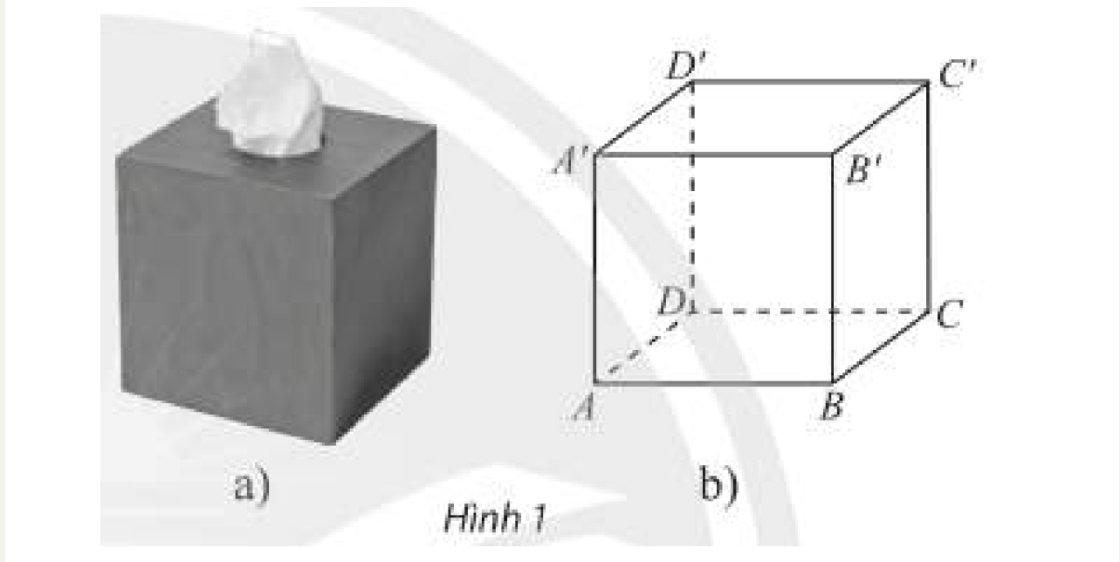
a: (ABC) và (ABD); (A'B'C') và (A'B'D'); (AA'B) và (AA'B'),...
b: Không có hai mp phân biệt nào có 1 điểm chung
c: (ABCD) và (A'B'C'D')
(ABB'A') và (CDD'C')
Đúng 0
Bình luận (0)
Mỗi ô vuông của bảng kích thước 10x10 ( 10 dòng, 10 cột ) được ghi một số nguyên dương không vượt quá 10 sao cho bất kì 2 số nào ghi trong 2 ô chung 1 cạnh hoặc 2 ô chung 1 đỉnh của bảng là hai số nguyên tố cùng nhau. Chứng minh rằng có số được ghi ít nhất 17 lần.
Trên mỗi hình vuông con, kích thước2x2 chỉ có không quá 1 số chia hết cho 2, cũng vậy, có không quá 1 số chia hết cho 3
Lát kín bảng bởi 25 hình vuông, kích thước 2x2, có nhiều nhất 25 số chia hết cho 2, có nhiều nhất 25 số chia hết cho 3. Do đó, có ít nhất 50 số còn lại không chia hết cho 2, cũng không chia hết cho 3. Vì vậy, chúng phải là một trong các số 1,5,7.
Từ đó, theo nguyên lý Dirichlet, có một số xuất hiện ít nhất 17 lần.
Trong các điều khẳng định sau đây, điều nào đúng?a) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại.b) Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.c) Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác cho trước.d) Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó.
Đọc tiếp
Trong các điều khẳng định sau đây, điều nào đúng?
a) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại.
b) Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
c) Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác cho trước.
d) Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó.
Câu a) đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Câu b) sai. Qua một điểm có vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu c) sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Câu d) sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.
Đúng 0
Bình luận (0)
Trong các điều khẳng định sau đây, điều nào là đúng ?
a) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại
b) Qua một điểm duy nhất một mặt phẳng vuông góc với một mặt phẳng khác
c) Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác
d) Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó
Đọc tiếp
Trong các điều khẳng định sau đây, điều nào là đúng ?
a) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại
b) Qua một điểm duy nhất một mặt phẳng vuông góc với một mặt phẳng khác
c) Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác
d) Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó
Câu a) đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Câu b) sai. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu c) sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Câu d) sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.
Đúng 0
Bình luận (0)
Chứng minh rằng mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất ba cạnh.
Lấy một đỉnh B tùy ý của hình đa diện (H). Gọi M 1 là một mặt của hình đa diện (H) chứa B. Gọi A, B, C là ba đỉnh liên tiếp của M 1 . Khi đó AB, BC là hai cạnh của (H). Gọi M 2 là mặt khác với M 1 và có chung cạnh AB với M 1 . Khi đó M 2 còn có ít nhất một đỉnh D sao cho A, B, D là ba đỉnh khác nhau liên tiếp của M 2 . Nếu D ≡ C thì M 1 và M 2 có hai cạnh chung AB và BC, điều này vô lí. Vậy D phải khác C. Do đó qua đỉnh B có ít nhất ba cạnh BA, BC và BD.
Đúng 0
Bình luận (0)
Cho các phát biểu sau:(1). Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.(2). Hai đa giác phân biệt của một hình đa diện chỉ có thể có thể hoặc không có điểm chung,hoặc chỉ có một đỉnh chung, hoặc một cạnh chung.(3). Mỗi cạnh của đa giác nào của một hình đa diện cũng là cạnh chung của đúng hai đa giác.Số phát biểu đúng là A. 0 B. 1 C. 3 D. 2
Đọc tiếp
Cho các phát biểu sau:
(1). Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
(2). Hai đa giác phân biệt của một hình đa diện chỉ có thể có thể hoặc không có điểm chung,
hoặc chỉ có một đỉnh chung, hoặc một cạnh chung.
(3). Mỗi cạnh của đa giác nào của một hình đa diện cũng là cạnh chung của đúng hai đa giác.
Số phát biểu đúng là
A. 0
B. 1
C. 3
D. 2
Cho các phát biểu sau: (1). Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia. (2). Hai đa giác phân biệt của một hình đa diện chỉ có thể có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc một cạnh chung. (3). Mỗi cạnh của đa giác nào của một hình đa diện cũng là cạnh chung của đúng hai đa giác. Số phát biểu đúng là A. 0 B. 1 C. 3 D. 2
Đọc tiếp
Cho các phát biểu sau:
(1). Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
(2). Hai đa giác phân biệt của một hình đa diện chỉ có thể có thể hoặc không có điểm chung,
hoặc chỉ có một đỉnh chung, hoặc một cạnh chung.
(3). Mỗi cạnh của đa giác nào của một hình đa diện cũng là cạnh chung của đúng hai đa giác.
Số phát biểu đúng là
A. 0
B. 1
C. 3
D. 2