Phương trình sin x - 1 sin x = sin 2 x - 1 sin 2 x có bao nhiêu nghiệm thuộc 0 ; 2018 π
A. 1008
B. 1009
C. 2018
D. 1010
Trong các phương trình sau: cos x = 5 - 3 (1); sin x = 1 - 2 (2); sin x + cos x = 2 (3), phương trình nào vô nghiệm?
A. (2)
B. (1)
C. (3)
D. (1) và (2)
Trong các phương trình sau: cos x = 5 - 3 (1); sin x = 1 - 2 (2); sin x + cos x = 2 (3), phương trình nào vô nghiệm?
A. (2).
B. (1).
C. (3).
D. (1) và (2).
Chọn C
Ta có: ![]() nên (1) và (2) có nghiệm.
nên (1) và (2) có nghiệm.
Cách 1:
Xét: ![]()
![]() nên (3) vô nghiệm.
nên (3) vô nghiệm.
Cách 2:
Điều kiện có nghiệm của phương trình: sin x + cos x = 2 là: 
(vô lý) nên (3) vô nghiệm.
Cách 3:
Vì 

nên (3) vô nghiệm.
Giải phương trình sau:
a, \(\sin\left(2x\right)+\sin\left(x\right)-\dfrac{1}{2\sin\left(x\right)}-\dfrac{1}{\sin\left(2x\right)}=2\cot\left(2x\right)\)
b, \(\left(\sin\left(2x\right)+cos\left(2x\right)\right)cos\left(x\right)+2cos\left(2x\right)-sin\left(x\right)=0\)
c, \(\sin\left(2x\right)-\cos\left(2x\right)+3\sin\left(x\right)-\cos\left(x\right)-1=0\)
b)
(sin2x + cos2x)cosx + 2cos2x - sinx = 0
⇔ cos2x (cosx + 2) + sinx (2cos2 x – 1) = 0
⇔ cos2x (cosx + 2) + sinx.cos2x = 0
⇔ cos2x (cosx + sinx + 2) = 0
⇔ cos2x = 0
⇔ 2x = 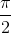 + kπ ⇔ x =
+ kπ ⇔ x = 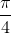 + k
+ k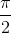 (k ∈
(k ∈ 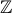 )
)
c)
Đáp án:
x=π6π6+ k2ππ
và x= 5π65π6+k2ππ (k∈Z)
Lời giải:
sin2x-cos2x+3sinx-cosx-1=0
⇔ 2sinxcosx-(1-2sin²x) +3sinx-cosx-1=0
⇔ 2sin²x+2sinxcosx+3sinx-cosx-2=0
⇔ (2sin²x+3sinx-2)+ cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+2)+cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+cosx+2)=0
⇔ sinx=1212
⇔ x=π6π6+ k2ππ
hoặc x= 5π65π6+k2ππ (k∈Z)
(sinx+cosx+2)=0 (vô nghiệm do sinx+cosx+2=√22sin(x+π4π4)+2>0)
Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
giải các phương trình sau : a). sin 2x+sin2 x=1/2
b.2sin2 x +3 sin x cosx + cos2 x= 0
c.sin2 x/2 + sin x - 2 cos 2 x/2 = 1/2
giải các phương trình sau :
1. sin( x+\(\pi\)/4)=2/3
2.cos2x-5sinx-3=0
3.cos3x=sin2x
4.cos3x=-\(\sqrt{ }\)3 với -\(\pi\)/2<x<0
5.4sin\(^4\)x + 12cos\(^2\)x=7
6.cot(x-1)=(cos2x)/(1+tanx) + sin\(^2\)x - 1/2sin2x
7.sin\(^2\)3x-cos\(^2\)4x=sin\(^2\)5x-cos\(^2\)6x
Giải các phương trình: sin x + cos x = 1 + sin x . cos x
sin x + cos x = 1 + sin x.cos x
⇔ sin x.cos x – sin x – cos x + 1 = 0
⇔ (sinx. cosx –sinx)- (cosx -1 ) =0
⇔ sinx. (cosx – 1) – (cosx -1) = 0
⇔ (sin x – 1)(cos x – 1) = 0
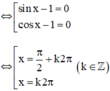
Vậy phương trình có tập nghiệm 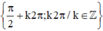
Có bao nhiêu số nguyên m để phương trình ln m + 2 sin x + ln m + 3 sin x = sin x có nghiệm thực ?
A. 4.
B. 3.
C. 5.
D. 6.
giải phương trình sin^2 x − 4√3 sin x · cos x + cos^2 x = −2.
Với \(cosx=0\) ko phải nghiệm
Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)
\(\Rightarrow tan^2x-4\sqrt{3}tanx+1=-2\left(1+tan^2x\right)\)
\(\Leftrightarrow3tan^2x-4\sqrt{3}tanx+3=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=\sqrt{3}\\tanx=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\\x=\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
Cho phương trình: cos 2 x + sin x - 1 = 0 * . Bằng cách đặt t = sin x - 1 ≤ x ≤ 1 thì phương trình (*) trở thành phương trình nào sau đây
A. - 2 t 2 + t = 0
B. t 2 + t + 2 = 0
C. - 2 t 2 + t - 2 = 0
D. - t 2 + t = 0