Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD bằng 5. Tính diện tích tam giác ABD
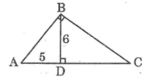
Đường cao BD của tâm giác nhọn ABC bằng 6; đoạn thẳng AD bằng 5.
a) Tính diện tích tam giác ABD
b) Tính AC, dùng các thông tin dưới đây nếu cần:
sinC=3/5, cosC=4/5, tgC=3/4.
Mọi người ơi e có 1 bài y như này mọi người vào trang của e xem giúp e với
GIÚP TÔI VỚI MAI TÔI PHẢI NỘP RỒI:
Đường cao BD của tam giác nhọn ABC bằng 6 ; đoạn thẳng AD bằng 5 .
a) tính diện tích tam giác ABD .
b) tính AC , dùng các thông tin dưới đây nếu cần :
sin C = 3/5, cos C = 4/5, tan C = 3/4
tinh ab bang pitago .su dung tam giac dong dang abd va abc suy ra ab2 =ad*ac the so roi tinh
a) Vì tam giác ABD vuông tại D nên ta có:
SΔABD=12.BD.AD=12.6.5=15 (đvdt)
b) Ta có: tgˆC=BD/DC
Theo giả thiết: tgˆC=3/4
Suy ra: BD/DC=34⇒DC=4/3BD=4.6/3=8
Suy ra: AC=AD+DC=5+8=13
Đường cao BD của tam giác nhọn ABC bằng 6; đoạn thẳng AD bằng 5
a) Tính diện tích tam giác ABD
b) Tính AC, dùng các thông tin dưới đây nếu cần :
\(\sin C=\dfrac{3}{5};\cos C=\dfrac{4}{5};tgC=\dfrac{3}{4}\)
Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD bằng 5. Tính AC, dùng các thông tin dưới đây nếu cần: sin ∠ C = 3 5 ; c o s ∠ C = 4 5 ; t g ∠ C = 3 4
Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD=5.
a)Tính diện tích tam giác ABC
b)Tính AC (sử dụng thông tin sau nếu cần: \(\sin C=\frac{3}{5}\),\(\cos C=\frac{4}{5}\),\(\tan C=\frac{3}{4}\).)
a) Vì tam giác ABD vuông tại D nên ta có:
SΔABD=12.BD.AD=12.6.5=15(đvdt)
b) Ta có: tgˆC=BD/DCt
Theo giả thiết: tgˆC=3/4
Suy ra: BD/DC=3/4⇒DC=4/3 BD=4.6/3=8
Suy ra: AC=AD+DC=5+8=13.
cho hình tam giác abc có ab =50cm ,bc=40cm ,nếu kéo dài bc thêm một đoạn cd =20 cm thì ta được tam giác abd cân [ có ab=ad] và tam giác acd có chiều cao ci =16cm.
a tính diện tích tam giác acd
b tính đường cao ah của tam giác abc
c so sánh diện tích tam giác acd và diện tích tam giác abd
d đường cao ci của tam giác adc bằng bao nhiêu % đường cao ck của tam giác acb?
cho tam giác ABC nhọn có góc A bằng 600 kẻ đường cao BD và CE, biết diện tích tam giác ABC bằng 24,42017 cm2 ,cạnh AB bằng 6,52 cm
a/ Tính độ dài cạnh AD và Đường caoCE
b/ Tính diện tích tam giác ADE
Cho ΔABC có 3 góc đều nhọn, hai đường cao BD và CE.
a) Chứng minh ΔADB ~ ΔAEC
b) Chứng minh ΔAED ~ ΔACB
c) Cho góc ABD bằng 60o và diện tích tam giác ABC bằng 120cm ². Tính diện tích của ΔADE
chỉ cần câu C thôi
a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)
b) Ta có: ΔADB\(\sim\)ΔAEC(cmt)
nên \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
hay \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét ΔAED và ΔACB có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)(cmt)
\(\widehat{A}\) chung
Do đó: ΔAED\(\sim\)ΔACB(c-g-c)
Cho tam giác ABC có AB = 12 cm BC = 14 cm AC bằng 9 cm B D là đường phân giác của góc B
a) Tính độ dài các đoạn thẳng AD và DC
b) Tính tỉ số diện tích của tam giác ABD và tam giác ADC
a: Xét ΔABC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
=>\(\dfrac{AD}{12}=\dfrac{CD}{14}\)
=>\(\dfrac{AD}{6}=\dfrac{CD}{7}\)
mà AD+CD=AC=9cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{7}=\dfrac{AD+CD}{6+7}=\dfrac{9}{13}\)
=>\(AD=\dfrac{9}{13}\cdot6=\dfrac{54}{13}\left(cm\right);CD=\dfrac{9}{13}\cdot7=\dfrac{63}{13}\left(cm\right)\)
b: Sửa đề: b) Tính tỉ số diện tích của tam giác ABD và tam giác BDC
Vì \(\dfrac{AD}{6}=\dfrac{CD}{7}\)
nên \(\dfrac{AD}{CD}=\dfrac{6}{7}\)
=>\(\dfrac{S_{ABD}}{S_{CBD}}=\dfrac{6}{7}\)
=>\(S_{ABD}=\dfrac{6}{7}\cdot S_{CBD}\)