Các câu hỏi tương tự
GIÚP TÔI VỚI MAI TÔI PHẢI NỘP RỒI:
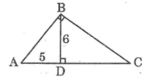
Đường cao BD của tam giác nhọn ABC bằng 6 ; đoạn thẳng AD bằng 5 .
a) tính diện tích tam giác ABD .
b) tính AC , dùng các thông tin dưới đây nếu cần :
sin C = 3/5, cos C = 4/5, tan C = 3/4
Đường cao BD của tâm giác nhọn ABC bằng 6; đoạn thẳng AD bằng 5.
a) Tính diện tích tam giác ABD
b) Tính AC, dùng các thông tin dưới đây nếu cần:
sinC=3/5, cosC=4/5, tgC=3/4.
Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD=5.
a)Tính diện tích tam giác ABC
b)Tính AC (sử dụng thông tin sau nếu cần: \(\sin C=\frac{3}{5}\),\(\cos C=\frac{4}{5}\),\(\tan C=\frac{3}{4}\).)
Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD bằng 5. Tính diện tích tam giác ABD
Cho tam giác ABC vuông tại A, đường cao AH.
a) Nếu sin ACB=3/5 và BC=20 cm. Giải tam giác ABC.
b) Đường thẳng vuông góc với BC tại B cắt đường thẳng AC tại D. c/m AD.AC=BH.BC
c) Kẻ tia phân giác BE của DBA . c/m \(tanEBA=\dfrac{AD}{AB+BD}\)
Cho tam giác ABC trong đó AB 5cm, AC 8cm, góc (BAC)
20
°
Tính diện tích tam giác ABC, có thể dùng các thông tin dưới đây nếu cần:sin
20
°
≈ 0,3420; cos
20
°
≈ 0,9397; tg
20
°
≈ 0,3640
Đọc tiếp
Cho tam giác ABC trong đó AB = 5cm, AC = 8cm, góc (BAC) = 20 °
Tính diện tích tam giác ABC, có thể dùng các thông tin dưới đây nếu cần:
sin 20 ° ≈ 0,3420; cos 20 ° ≈ 0,9397; tg 20 ° ≈ 0,3640
Cho tam giác ABC nhọn nội tiếp (O;R). Các đường cao BB',CC' của tam giác cắt nhau ở H. Vẽ đường kính AD của đường tròn.AH cắt (O) tại E
1)C/m BCDE là hình thang cân
2)C/m BHCD là hình bình hành
3)Gọi I là trung điểm BC.C/m AH=2OI
4)Gọi G là trọng tâm tam giác ABC. C/m 3 điểm H,G,O thẳng hàng
5) Đặt BC=a,CA=b,Ab=c.C/m SABC=abc chia 4R
Cho tam giác ABC vuông tại A có AB : AC 4 : 5 và đường cao AH bằng 12cm. Khi đó độ dài đoạn thẳng HB bằngA. 6cm; B. 9,6cm; C. 12cm; D. 15cm.Hãy chọn phương án đúng.*Trong các bài (1.3, 1.4, 1.5) ta sẽ sử dụng các kí hiệu sau đây đối với tam giác ABC vuông tại A có đường cao AH:AB c, AC b, BC a, AH h, BH c’, CH b’.
Đọc tiếp
Cho tam giác ABC vuông tại A có AB : AC = 4 : 5 và đường cao AH bằng 12cm. Khi đó độ dài đoạn thẳng HB bằng
A. 6cm; B. 9,6cm; C. 12cm; D. 15cm.
Hãy chọn phương án đúng.
*Trong các bài (1.3, 1.4, 1.5) ta sẽ sử dụng các kí hiệu sau đây đối với tam giác ABC vuông tại A có đường cao AH:
AB = c, AC = b, BC = a, AH = h, BH = c’, CH = b’.
1) Với mọi góc nhọn alpha, chứng minh 4sin^3alpha-4sin^2alpha+102) Delta ABCnhọn có ABc, BCa, CAb, chu vi bằng 2p, diện tích bằng S, góc B bằng 2alpha. Chứng minh sin A:tanalpha theo p, b và c.3) Delta ABCnhọn có ABc, BCa, CAb.Tìm giá trị lớn nhất của sin(A/2)4)Hính thoi ABCD có H là giao điểm hai đường chép, Trung trực của AB cắt AC tại E, cắt BD tại F. Tính AH:BH và diện tích ABCD theo EA và FB.5) Chứng minh tron tất cả các tam giác cân có cùng diện tích thì tam giác nào có đáy nhỏ nhất thì là...
Đọc tiếp
1) Với mọi góc nhọn \(\alpha\), chứng minh \(4\sin^3\alpha-4\sin^2\alpha+1>0\)
2) \(\Delta ABC\)nhọn có AB=c, BC=a, CA=b, chu vi bằng 2p, diện tích bằng S, góc B bằng \(2\alpha\). Chứng minh \(\sin A:\tan\alpha\) theo p, b và c.
3) \(\Delta ABC\)nhọn có AB=c, BC=a, CA=b.Tìm giá trị lớn nhất của sin(A/2)
4)Hính thoi ABCD có H là giao điểm hai đường chép, Trung trực của AB cắt AC tại E, cắt BD tại F. Tính AH:BH và diện tích ABCD theo EA và FB.
5) Chứng minh tron tất cả các tam giác cân có cùng diện tích thì tam giác nào có đáy nhỏ nhất thì là tam giác đó có góc ở đỉnh nhỏ nhất.










